About harmonic microchromatics

How many colors are there in a rainbow?

Seven – our compatriots will confidently answer.

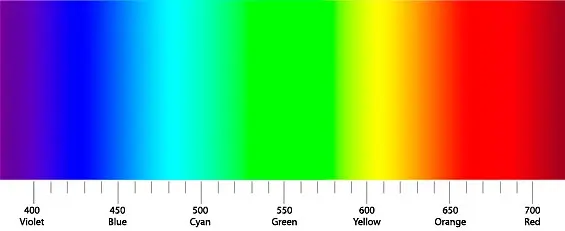
But the computer screen is capable of reproducing only 3 colors, known to all – RGB, that is, red, green and blue. This does not prevent us from seeing the entire rainbow in the next figure (Fig. 1).

In English, for example, for two colors – blue and cyan – there is only one word blue. And the ancient Greeks did not have a word for blue at all. The Japanese don’t have a designation for green. Many peoples “see” only three colors in the rainbow, and some even two.

What is the correct answer to this question?

If we look at Fig. 1, we will see that the colors pass into each other smoothly, and the boundaries between them are just a matter of agreement. There is an infinite number of colors in the rainbow, which people of different cultures divide by conditional boundaries into several “generally accepted” ones.

How many notes are in an octave?

A person who is superficially familiar with music will answer – seven. People with a musical education, of course, will say – twelve.

But the truth is that the number of notes is just a matter of language. For peoples whose musical culture is limited to the pentatonic scale, the number of notes will be five, in the classical European tradition there are twelve, and, for example, in Indian music twenty-two (in different schools in different ways).

The pitch of a sound or, scientifically speaking, the frequency of vibrations is a quantity that changes continuously. Between note A, sounding at a frequency of 440 Hz, and a note si-flat at a frequency of 466 Hz there is an infinite number of sounds, each of which we can use in musical practice.

Just as a good artist does not have 7 fixed colors in his picture, but a huge variety of shades, so the composer can safely operate not only with sounds from the 12-note equal temperament scale (RTS-12), but with any other sounds of his choice.

fees

What stops most composers?

First, of course, the convenience of execution and notation. Almost all instruments are tuned in the RTS-12, almost all musicians learn to read classical notation, and most listeners are used to music consisting of “ordinary” notes.

The following can be objected to this: on the one hand, the development of computer technology makes it possible to operate with sounds of almost any height and even any structure. On the other hand, as we saw in the article on dissonances, over time, listeners become more and more loyal to the unusual, more and more complex harmonies penetrate the music, which the public understands and accepts.

But there is a second difficulty on this path, perhaps even more significant.

The fact is that as soon as we go beyond 12 notes, we practically lose all reference points.

Which consonances are consonant and which are not?

Will gravity exist?

On what will harmony be built?

Will there be something similar to keys or modes?

Microchromatic

Of course, only musical practice will give full answers to the questions posed. But we already have some devices for orienteering on the ground.

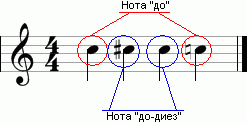
First, it is necessary to somehow name the area where we are going. Usually, all musical systems that use more than 12 notes per octave are classified as microchromatic. Sometimes systems in which the number of notes is (or even less than) 12 are also included in the same area, but these notes differ from the usual RTS-12. For example, when using the Pythagorean or natural scale, one can say that microchromatic changes are made to the notes, implying that these are notes almost equal to the RTS-12, but quite a bit away from them (Fig. 2).

In Fig. 2 we see these small changes, for example, the note h Pythagorean scale just above the note h from RTS-12, and natural h, on the contrary, is somewhat lower.

But the Pythagorean and natural tunings preceded the appearance of the RTS-12. For them, their own works were composed, a theory was developed, and even in previous notes we touched on their structure in passing.

We want to go further.

Are there any reasons forcing us to move away from the familiar, convenient, logical RTS-12 into the unknown and strange?

We will not dwell on such prosaic reasons as the familiarity of all roads and paths in our usual system. Let’s better accept the fact that in any creativity there must be a share of adventurism, and let’s hit the road.

Compass

An important part of musical drama is such a thing as consonance. It is the alternation of consonances and dissonances that gives rise to gravity in music, a sense of movement, development.

Can we define consonance for microchromatic harmonies?

Recall the formula from the article about consonance:

This formula allows you to calculate the consonance of any interval, not necessarily the classical one.

If we calculate the consonance of the interval from to to all sounds within one octave, we get the following picture (Fig. 3).

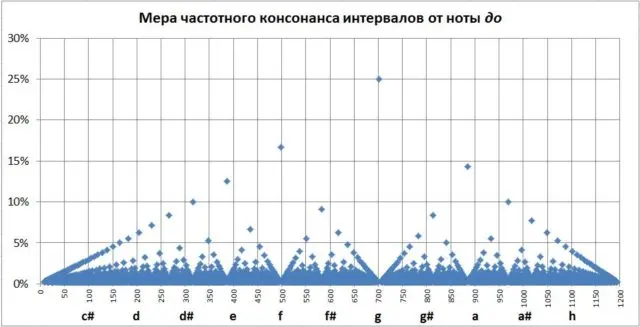
The width of the interval is plotted horizontally here in cents (when cents are a multiple of 100, we get into a regular note from the RTS-12), vertically – the measure of consonance: the higher the point, the more consonant such an interval sounds.

Such a graph will help us navigate the microchromatic intervals.

If necessary, you can derive a formula for the consonance of chords, but it will look much more complicated. To simplify, we can remember that any chord consists of intervals, and the consonance of a chord can be estimated quite accurately by knowing the consonance of all the intervals that form it.

Local map

Musical harmony is not limited to the understanding of consonance.

For example, you can find a consonant more consonant than a minor triad, however, it plays a special role due to its structure. We studied this structure in one of the previous notes.

It is convenient to consider the harmonic features of music in space of multiplicities, or PC for short.

Let us briefly recall how it is constructed in the classical case.

We have three simple ways to connect two sounds: multiplication by 2, multiplication by 3 and multiplication by 5. These methods generate three axes in the space of multiplicities (PC). Each step along any axis is a multiplication by the corresponding multiplicity (Fig. 4).

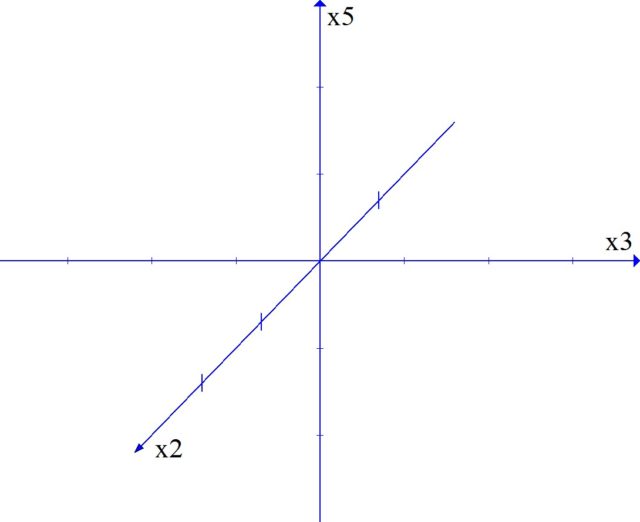
In this space, the closer the notes are to each other, the more consonant they will form.

All harmonic constructions: frets, keys, chords, functions acquire a visual geometric representation in the PC.

You can see that we take prime numbers as multiplicity factors: 2, 3, 5. A prime number is a mathematical term meaning that a number is only divisible by 1 and itself.

This choice of multiplicities is quite justified. If we add an axis with a “non-simple” multiplicity to the PC, then we will not get new notes. For example, each step along the axis of multiplicity 6 is, by definition, a multiplication by 6, but 6=2*3, therefore, we could get all these notes by multiplying 2 and 3, that is, we already had all of them without this axes. But, for example, getting 5 by multiplying 2 and 3 will not work, therefore, the notes on the axis of multiplicity 5 will be fundamentally new.

So, in a PC it makes sense to add axes of simple multiplicities.

The next prime number after 2, 3 and 5 is 7. It is this one that should be used for further harmonic constructions.

If the note frequency to we multiply by 7 (we take 1 step along the new axis), and then octave (divide by 2) transfer the resulting sound to the original octave, we get a completely new sound that is not used in classical musical systems.

An interval consisting of to and this note will sound like this:

The size of this interval is 969 cents (a cent is 1/100 of a semitone). This interval is somewhat narrower than a small seventh (1000 cents).

In Fig. 3 you can see the point corresponding to this interval (below it is highlighted in red).

The measure of consonance of this interval is 10%. For comparison, a minor third has the same consonance, and a minor seventh (both natural and Pythagorean) is an interval less consonant than this one. It is worth mentioning that we mean calculated consonance. Perceived consonance may be somewhat different, as a small seventh for our hearing, the interval is much more familiar.

Where will this new note be located on the PC? What harmony can we build with it?

If we take out the octave axis (the axis of multiplicity 2), then the classical PC will turn out to be flat (Fig. 5).

All notes located in an octave to each other are called the same, so such a reduction is to a certain extent legitimate.

What happens when you add a multiplicity of 7?

As we noted above, the new multiplicity gives rise to a new axis in the PC (Fig. 6).

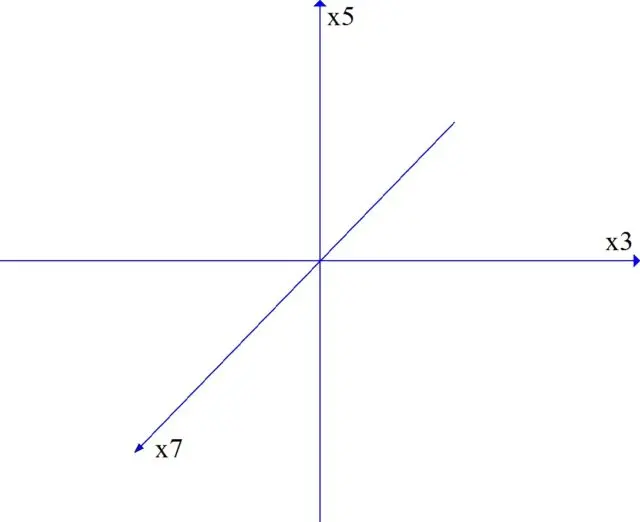
The space becomes three-dimensional.

This provides a huge number of possibilities.

For example, you can build chords in different planes (Fig. 7).

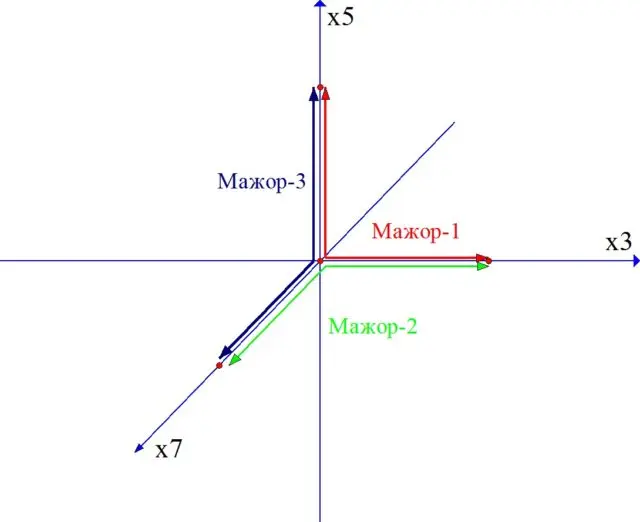
In a piece of music, you can move from one plane to another, build unexpected connections and counterpoints.

But in addition, it is possible to go beyond flat figures and build three-dimensional objects: with the help of chords or with the help of movement in different directions.

Playing with 3D figures, apparently, will be the basis for harmonic microchromatics.

Here is an analogy in this connection.

At that moment, when music moved from the “linear” Pythagorean system to the “flat” natural one, that is, it changed the dimension from 1 to 2, music underwent one of the most fundamental revolutions. Tonalities, full-fledged polyphony, the functionality of chords and an innumerable number of other expressive means appeared. The music was practically reborn.

Now we are facing the second revolution – microchromatic – when the dimension changes from 2 to 3.

Just as the people of the Middle Ages could not predict what “flat music” would be like, so it is difficult for us now to imagine what three-dimensional music will be like.

Let’s live and hear.

Author — Roman Oleinikov