New Keys

On the night of September 23-24, Johann Franz Encke, who had just celebrated his 55th birthday, was knocked persistently at the house. Heinrich d’Arre, a student out of breath, stood at the door. Having exchanged a couple of phrases with the visitor, Encke quickly got ready, and the two of them went to the Berlin Observatory headed by Encke, where an equally excited Johann Galle was waiting for them near the reflecting telescope.

Observations, to which the hero of the day joined in this way, lasted until half past three in the night. So in 1846, the eighth planet of the solar system, Neptune, was discovered.

But the discovery made by these astronomers changed little more than our understanding of the world around us.

Theory and practice

The apparent size of Neptune is less than 3 arc seconds. To understand what this means, imagine that you are looking at a circle from its center. Divide the circle into 360 parts (Fig. 1).

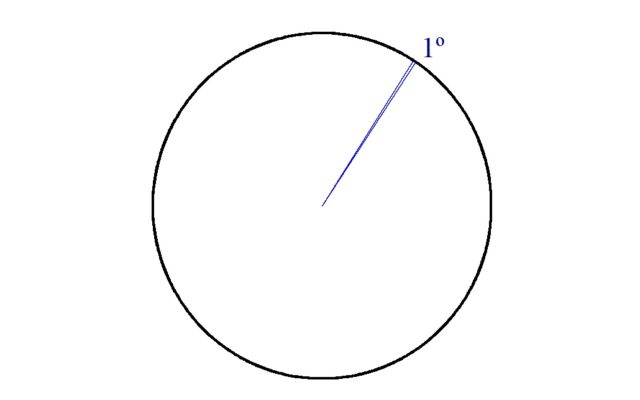
The angle we got in this way is 1° (one degree). Now divide this thin sector into another 60 parts (it is no longer possible to depict this in the figure). Each such part will be 1 arc minute. And finally, we divide by 60 and an arc minute – we get an arc second.

How did astronomers find such a microscopic object in the sky, less than 3 arc seconds in size? The point is not the power of the telescope, but how to choose the direction on the huge celestial sphere where to look for a new planet.

The answer is simple: the observers were told this direction. The teller is usually called the French mathematician Urbain Le Verrier, it was he who, observing the anomalies in the behavior of Uranus, suggested that there is another planet behind him, which, attracting Uranus to itself, causes it to deviate from the “correct” trajectory. Le Verrier not only made such an assumption, but was able to calculate where this planet should be, wrote about this to Johann Galle, for whom after that the search area drastically narrowed.

So Neptune became the first planet that was first predicted by theory, and only then found in practice. Such a discovery was called “the discovery at the tip of the pen”, and it forever changed the attitude towards scientific theory as such. Scientific theory has ceased to be understood as just a game of the mind, at best describing “what is”; scientific theory has clearly demonstrated its predictive ability.

Through the stars to the musicians

Let’s get back to music. As you know, there are 12 notes in an octave. How many three-sound chords can be built from them? It is easy to count – there will be 220 such chords.

This, of course, is not an astronomically huge number, but even in such a number of consonances it is quite easy to get confused.

Fortunately, we have a scientific theory of harmony, we have a “map of the area” – the space of multiplicities (PC). How a PC is built, we considered in one of the previous notes. Moreover, we saw how the usual keys are obtained in the PC – major and minor.

Let us single out once again those principles that underlie traditional keys.

This is how major and minor look like in PC (fig. 2 and fig. 3).

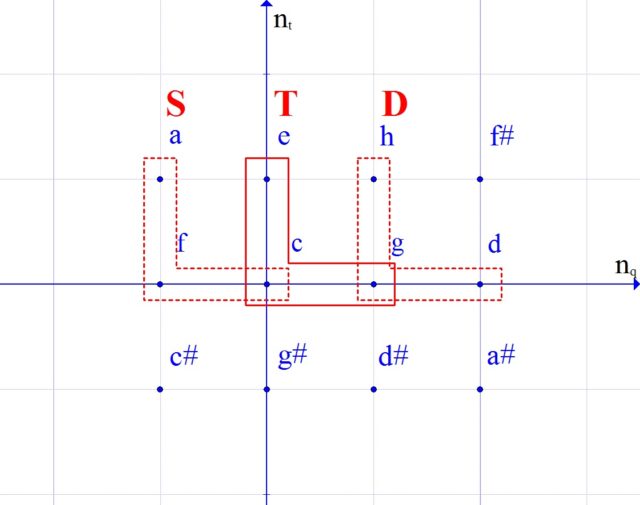
The central element of such constructions is a corner: either with rays directed upwards – a major triad, or with rays directed downwards – a minor triad (Fig. 4).

These corners form a crosshair, which allows you to “centralize” one of the sounds, make it “main”. This is how the tonic appears.

Then such a corner is copied symmetrically, in the most harmonically close sounds. This copying gives rise to a subdominant and a dominant.

Tonic (T), subdominant (S) and dominant (D) are called the main functions in the key. The notes included in these three corners form the scale of the corresponding key.

By the way, in addition to the main functions in the key, side chords are usually distinguished. We can depict them in PC (Fig. 5).

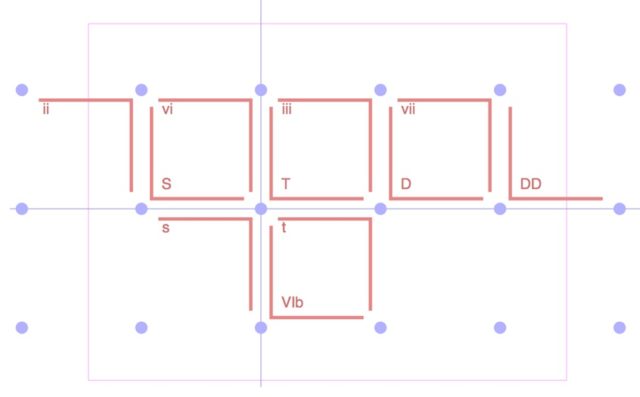
Here DD is a double dominant, iii is a function of the third step, VIb is a reduced sixth, and so on. We see that they are the same major and minor corners, located not far from the tonic.

Any note can act as a tonic, functions will be built from it. The structure – the relative position of the corners in the PC – will not change, it will simply move to another point.

Well, we have analyzed how traditional tonalities are harmoniously arranged. Will we find, looking at them, the direction where it is worth looking for “new planets”?

I think that we will find a couple of celestial bodies.

Let’s look at fig. 4. It shows how we have centralized the sound with the triad corner. In one case, both beams were directed upwards, in the other – downwards.

It seems that we missed two more options, no worse than centralizing the note. Let us have one ray pointing up and the other down. Then we get these corners (Fig. 6).

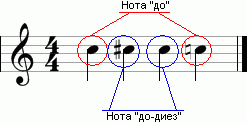
These triads centralize the note, but in a rather unusual way. If you build them from notes to, then on the stave they will look like this (Fig. 7).

We will keep all further principles of tonality construction unchanged: we will add two similar corners symmetrically in the nearest notes.

Will get new keys (Fig. 8).

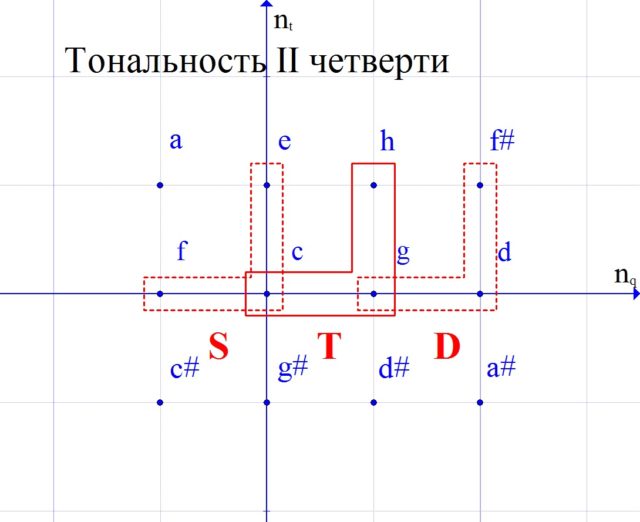
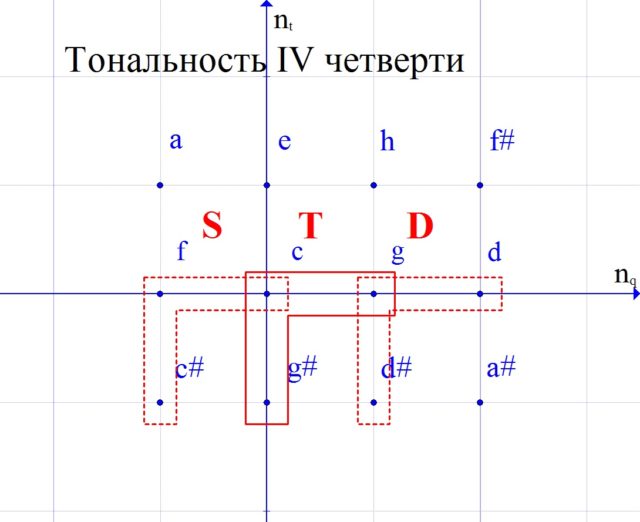
Let’s write down their scales for clarity.

We have depicted notes with sharps, but, of course, in some cases it will be more convenient to rewrite them with enharmonic flats.

The main functions of these keys are shown in fig. 8, but the side chords are missing to complete the picture. By analogy with Fig. 5 we can easily draw them in a PC (Fig. 10).

Let’s write them out on the music staff (Fig. 11).

Comparing the gamma in Fig. 9 and function names in fig. 11, you can see that the binding to the steps here is rather arbitrary, it “left by inheritance” from the traditional keys. In fact, the function of the third degree can be built not at all from the third note in the scale, the function of the reduced sixth – not at all from the reduced sixth, etc. What, then, do these names mean? These names determine the functional meaning of a particular triad. That is, the function of the third step in the new key will perform the same role that the function of the third step performed in major or minor, despite the fact that it differs quite significantly structurally: the triad is used differently and it is located in a different place on the scale.

Perhaps it remains to highlight two theoretical questions

The first one is connected with the tonality of the second quarter. We see that by actually centralizing the note salt, its tonic corner is built from to (to – lower sound in a chord). Also from to the scale of this tonality begins. And in general, the tonality that we have depicted should be called the tonality of the second quarter of to. This is rather strange at first glance. However, if we look at Fig. 3, we will find that we have already met the same “shift” in the most ordinary minor. In this sense, nothing extraordinary happens in the key of the second quarter.

The second question: why such a name – the keys of II and IV quarters?

In mathematics, two axes divide the plane into 4 quarters, which are usually numbered counterclockwise (Fig. 12).

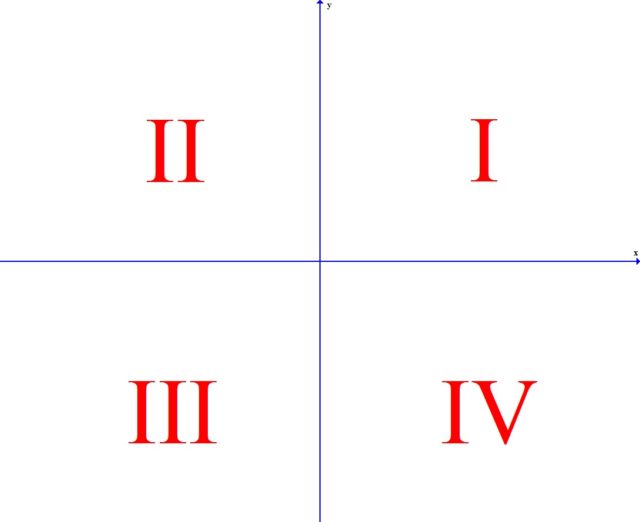
We look where the rays of the corresponding corner are directed, and we call the keys according to this quarter. In this case, the major will be the key of the first quarter, the minor will be the third quarter, and the two new keys, respectively, II and IV.

Set up telescopes

As a dessert, let’s listen to a small etude written by the composer Ivan Soshinsky in the key of the fourth quarter.

“Etulle” I. Soshinsky

Are the four keys we got the only ones possible? Strictly speaking, no. Strictly speaking, tonal constructions are generally not necessary for the creation of musical systems, we can use other principles that have nothing to do with centralization or symmetry.

But we will postpone the story about other options for now.

It seems to me that another aspect is important. All theoretical constructs make sense only when they pass from theory to practice, to culture. How temperament was fixed in music only after the writing of the Well-Tempered Clavier by J.S. Bach and any other systems will matter as they move from paper to scores, to concert halls, and ultimately to the musical experience of listeners.

Well, let’s set up our telescopes and see if composers can prove themselves as pioneers and colonizers of new musical worlds.

Author — Roman Oleinikov