Lesson 1
Contents
To understand the basics of music theory and master musical literacy, we need to understand what sound is. Actually, sound is the basis of music, without it music will be impossible.
In addition, you need to get an idea about the note-octave system. This is all directly related to the properties of sound.
As you can see, in the first lesson we have an extensive program waiting for us, and we are sure that you will cope with it! So let’s get started.
Physical properties of sound
First, let’s study the properties of sound from the point of view of physics:
Sound – This is a physical phenomenon, which is a mechanical wave vibration that propagates in a particular medium, most often in the air.
Sound has physical properties: pitch, strength (loudness), sound spectrum (timbre).
Basic physical properties of sound:
| ✔ | Height is determined by the frequency of oscillation and is expressed in hertz (Hz). |
| ✔ | sound power (loudness) is determined by the amplitude of vibrations and is expressed in decibels (dB). |
| ✔ | Sound spectrum (timbre) depends on additional vibrational waves or overtones that are formed simultaneously with the main vibrations. This is well heard in music and singing. |
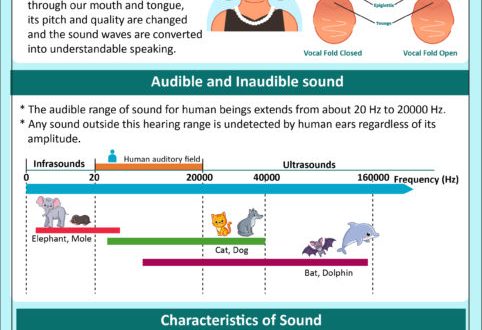
The term “overtone” comes from two English words: over – “above”, tone – “tone”. From their addition, the word overtone or “overtone” is obtained. Human hearing is capable of perceiving sounds with a frequency of 16-20 hertz (Hz) and a volume of 000-10 dB.
To make it easier to navigate, let’s say that 10 dB is a rustle, and 130 dB is the sound of an airplane taking off, if you hear it close. 120-130 dB is the level of the pain threshold, when it is already uncomfortable for the human ear to hear the sound.
In terms of height, the range from 30 Hz to about 4000 Hz is considered comfortable. We will return to this topic when we talk about the musical system and the scale. Now it is important to remember that the pitch and the loudness of the sound are fundamentally different things. In the meantime, let’s talk about the properties of musical sound.
Music Sound Properties
How is musical sound different from any other? This is a sound with identical and uniformly repeating (i.e. periodic) wave oscillations. Sound with non-periodic, i.e. unequal and unevenly repeating vibrations, do not belong to the musical. These are noise, whistling, howling, rustling, roaring, squeaking and many other sounds.
In other words, musical sound has all the same properties as any other, i.e. has a pitch, loudness, timbre, but only a certain combination of these properties allows us to classify the sound as musical. What else, besides periodicity, matters for musical sound?
Firstly, not the entire audible range is considered musical, which we will discuss in more detail later. Secondly, for a musical sound, its duration is important. This or that sound duration at a certain height allows you to emphasize the music or, conversely, leave the sound smooth. A short sound at the end allows you to put a logical point in a piece of music, and a long one – to leave a feeling of understatement in the listeners.
Actually the duration of the sound depends on the duration of the wave oscillations. The longer the wave vibrations go, the longer the sound is heard. To understand the relationship between the duration of a musical sound and its other characteristics, it is worth dwelling on such an aspect as the source of musical sound.
Sources of musical sound
If the sound is produced by a musical instrument, its basic physical characteristics do not depend in any way on the duration of the sound. The sound at the desired pitch will go exactly as long as you hold down the desired key of the synthesizer. The sound at the set volume will continue until you decrease or increase the volume on the synthesizer or electric guitar sound combo amplifier.
If we are talking about a singing voice, then the properties of musical sound interact more complicated. When is it easier to keep the sound at the right height without losing its power? Then, when you pull the sound for a long time or when you need to give it literally for a second? To draw a musical sound for a long time without losing the sound quality, its height and strength is a special art. If you want to find a beautiful voice and learn how to sing, we recommend that you study our online course “Voice and Speech Development”.
Music system and scale
For a deeper understanding of the properties of musical sound, we need a few more concepts. In particular, such as the musical system and the scale:
| ✔ | Music system – a set of sounds used in music of a certain height. |
| ✔ | Sound sequence – These are the sounds of the musical system, going in ascending or descending order. |
The modern musical system includes 88 sounds of different heights. They can be executed in ascending or descending order. The most clear demonstration of the relationship between the musical system and the scale is the piano keyboard.
The 88 piano keys (36 black and 52 white – we’ll explain why later) cover sounds from 27,5 Hz to 4186 Hz. Such acoustic capabilities are sufficient to perform any melody that is comfortable for the human ear. Sounds outside this range are practically not used in modern music.
The scale is built on certain regularities. Sounds whose frequency differs by 2 times (2 times higher or lower) are perceived by ear as similar. To make it easier to navigate, such concepts as scale steps, octave, tone and semitone are introduced into the theory of music.
Scale steps, octave, tone and semitone
Each musical sound of the scale is called a step. The distance between similar sounds (scale steps) that differ in height by 2 times is called an octave. The distance between adjacent sounds (steps) is a semitone. Semitones within an octave are equal (remember, this is important). Two semitones form a tone.
Names have been assigned to the main steps of the scale. These are “do”, “re”, “mi”, “fa”, “sol”, “la”, “si”. As you understand, these are 7 notes that we have known since childhood. On the piano keyboard, they can be found by pressing white keys:

Do not look at numbers and Latin letters yet. Look at the keyboard and the signed steps of the scale, they are also notes. You can see that there are 52 white keys, and only 7 names of the steps. This is precisely due to the fact that the steps that have a similar sound due to the difference in height by exactly 2 times are assigned the same names.
If we press 7 piano keys in a row, the 8th key will be named exactly as the one we pressed first. And, accordingly, to produce a similar sound, but at twice the height or less height, depending on which direction we were moving. The exact tuning frequencies of the piano can be found in a special table.
One more clarification of the terms is required here. An octave refers not only to the distance between similar sounds (scale steps), which differ in height by 2 times, but also 12 semitones from the note “to”.
You can find other definitions of the term “octave” used in music theory. But, because the purpose of our course is to give the basics of musical literacy, we will not go deep into theory, but will limit ourselves to the practical knowledge that you need to learn music and vocals.
For clarity and explanation of the applied meanings of the term, we will again use the piano keyboard and see that an octave is 7 white keys and 5 black keys.
Why do you need black keys on the piano
Here we, as promised earlier, will explain why the piano has 52 white keys and only 36 black ones. This will help you better understand the steps of the scale and semitones. The fact is that the distances in semitones between the main steps of the scale differ. For example, between steps (notes) “to” and “re”, “re” and “mi” we see 2 semitones, i.e. a black key between two white keys, and between “mi” and “fa” there is only 1 semitone, i.e. white keys are consecutive. Similarly, there is only 1 semitone between the “si” and “do” steps.
In total, 5 steps (notes) have distances of 2 semitones, and two steps (notes) have a distance of 1 semitone. It turns out the following arithmetic:
So we got 12 semitones in an octave. The piano keyboard holds 7 full octaves and 4 more semitones: 3 on the left (where the lowest sounds) and 1 on the right (high sound). We count everything semitones and keysresponsible for them:
So we got the total number of piano keys. We understand further. We have already learned that there are 7 white keys and 5 black keys in each octave. Beyond the full 7 octaves, we have 3 more white and 1 black keys. We count first white keys:
Now we count black keys:
Here are our 36 black keys and 52 white keys.
It seems that you have figured out the steps of the scale, octaves, tones and semitones. Remember this information, as it will come in handy in the next lesson, when we move on to a detailed study of musical notation. And this information will be needed in the last lesson, when we learn to play the piano.
Let’s clarify one more point. The regularities of building a scale are the same for all musical sounds, whether they are extracted using the piano, guitar or singing voice. We used the piano keyboard to explain the material solely because of greater clarity.
In the same way, we will use the piano to understand the note-octave system in more detail. This needs to be done in today’s lesson, because. on the next we will move on to musical notation and notation of notes on the stave.
Note-octave system
In general, the range of sounds potentially audible to the human ear covers almost 11 octaves. Because our course is devoted to musical literacy, we are only interested in musical sounds, i.e. about 9 octaves. To make it easier to remember octaves and their corresponding pitch ranges, we recommend going from top to bottom, i.e. from the upper range of sounds to the lower. The pitch in hertz for each octave will be indicated in the binary system for ease of remembering.
Octaves (names) and ranges:
It makes no sense to consider other octaves in the context of musical sounds. Thus, the highest note for men is F sharp of the 5th octave (5989 Hz), and this record was set by Amirhossein Molai on July 31, 2019 in Tehran (Iran) [Guinness World Records, 2019]. Singer Dimash from Kazakhstan reaches the note “re” in the 5th octave (4698 Hz). And sounds with a height below 16 Hz cannot be perceived by the human ear. You can study the complete table of correspondence of notes to frequencies and octaves at the following picture:
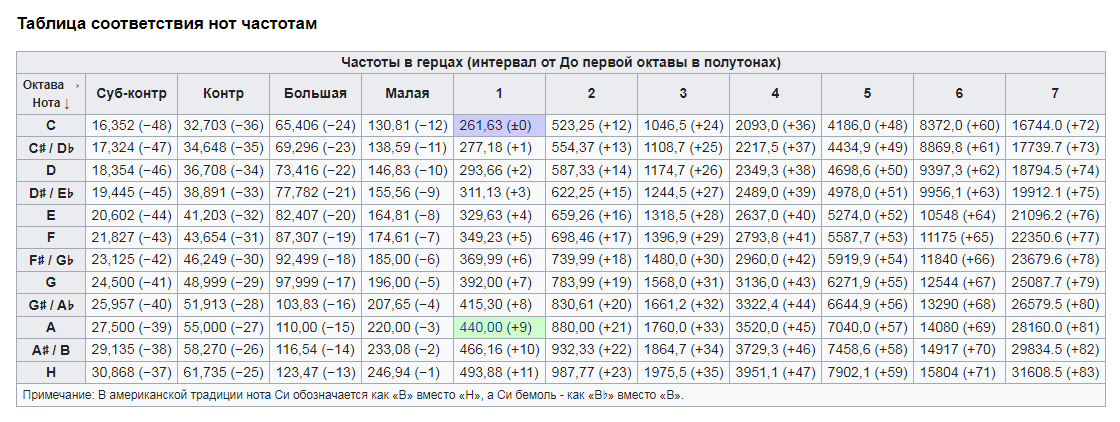
The 1st note of the first octave is highlighted in purple, i.e. note “do”, and green – note “la” of the first octave. It was on her, i.e. to a frequency of 440 Hz, by default all tuners for measuring the pitch are pre-installed.
Notes in octave: designation options
Today, different methods are used to denote the belonging of a note (pitch) to different octaves. The easiest way is to write down the names of the notes as they are: “do”, “re”, “mi”, “fa”, “sol”, “la”, “si”.
The second option is the so-called “Helmholtz notation”. This method involves the designation of notes in Latin letters, and belonging to the octave – in numbers. Let’s start with the notes.
Helmholtz sheet music:
It is also important to note that the note “si” can sometimes be represented not by the letter B, but by the letter H. The letter H is traditional for classical music, while the letter B is considered a more modern option. In our course, you will find both variations, so remember that both B and H stand for “si”.
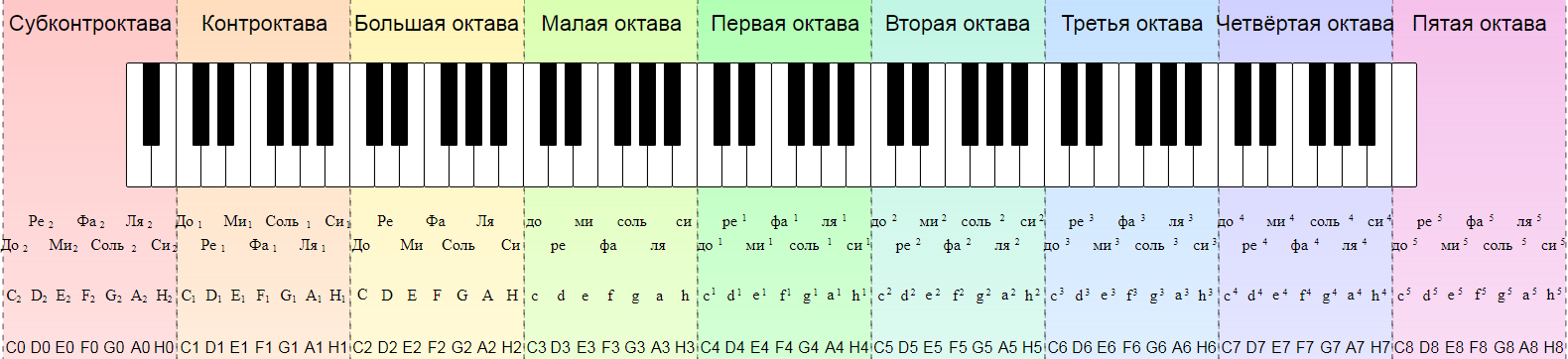
Now to octaves. Notes in the first to fifth octaves are written in small Latin letters and are indicated by numbers from 1 to 5. Notes of a small octave are in small Latin letters without numbers. Remember the association: small octave – small letters. Notes of a large octave are written in capital Latin letters. Remember: big octave – big letters. The notes of the contra-octave and sub-contra-octave are written in capital letters and the numbers 1 and 2, respectively.
Notes in octaves according to Helmholtz:
If anyone is surprised why the first note of the octave is not indicated by the first letter of the Latin alphabet, we will tell you that once upon a time the countdown began with the note “la”, behind which the designation A was fixed. However, then they decided to start the octave count from the note “to” , which has already been assigned the designation C. In order to avoid confusion in musical notations, we decided to keep the letter designations of notes as they are.
You can find more details about Helmholtz’s notation and other ideas in his work, available in Russian under the title “The doctrine of auditory sensations as a physiological basis for the theory of music” [G. Helmholtz, 2013].
And finally, the scientific notation, which was developed by the American Acoustic Society in 1939 and which is also relevant to this day. Notes are indicated by capital Latin letters, and belonging to the octave – by numbers from 0 to 8.
Scientific notation:
Please note that the numbers do not match the names of octaves from the first to the fifth. This circumstance often misleads even manufacturers of specialized programs for musicians. Therefore, in case of doubt, always check the sound and pitch of the note with the tuner. To do this, download the Pano Tuner mobile application and allow it access to the microphone.
It remains to add that for the first time the system of scientific notation was published in the July issue of The Journal of the Acoustical Society of America (Journal of the Acoustical Society of America) [The Journal of the Acoustical Society of America, 1939].
Now let’s summarize all currently accepted note notation systems for each octave. To do this, we will once again duplicate the picture already familiar to you with the piano keyboard and the designations of the steps of the scale (notes), but with the recommendation to pay attention to numeric and alphabetic designations:
And, finally, for the most complete understanding of the basic information of music theory, we should understand the varieties of tones and semitones.
Varieties of tones and semitones
Let’s say right away that from an applied point of view, this information will not be particularly useful to you for playing musical instruments or teaching vocals. However, terms denoting types of tones and semitones can be found in specialized literature. Therefore, you need to have an idea about them so as not to dwell on incomprehensible moments while reading literature or in-depth study of musical material.
Tone (kinds):
Halftone (kinds):
As you can see, the names are repeated, so it will not be difficult to remember. So, let’s figure it out!
Diatonic semitone (types):
Some examples you can see on the picture:

Chromatic semitone (types):

Diatonic tone (types):
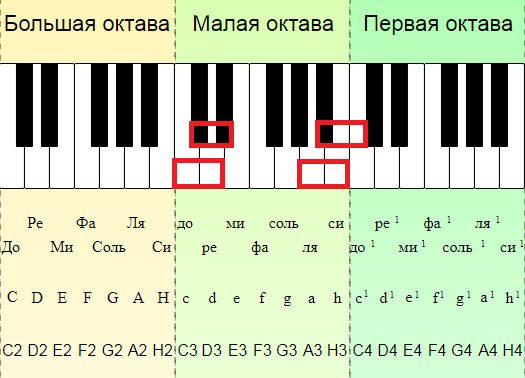
Chromatic tone (types):
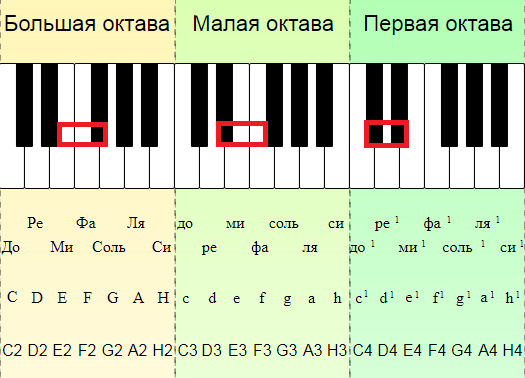
Let’s clarify that the examples are taken from the textbook by Varfolomey Vakhromeev “Elementary Theory of Music” and are shown on the piano keyboard for clarity, because. we will study the stave only in the next lesson, and we need the concepts of tone and semitone already now [V. Vakhromeev, 1961]. In general, we will repeatedly refer to the works of this great Russian teacher and musicologist throughout our course.
By the way, in 1984, a few months before his death, Varfolomey Vakhromeev was awarded the Order of the Holy Equal-to-the-Apostles Prince Vladimir of the 2nd degree for the “Textbook of Church Singing” he compiled for the theological schools of the Russian Orthodox Church. The textbook went through several reprints after his death [V. Vakhromeev, 2013].
An increase of 2 semitones is indicated by a double sharp or double sharp, a decrease of 2 semitones is indicated by a double flat or double flat. For double sharp there is a special icon, similar to a cross, but, because it is difficult to pick it up on the keyboard, the notation ♯♯ or just two pound signs ## can be used. It is easier with double-flats, they write either 2 ♭♭ signs or Latin letters bb.
And finally, the last thing you need to talk about in the topic “Properties of sound” is the anharmonicity of sounds. You learned earlier that semitones within an octave are equal. Therefore, a sound lowered by a semitone relative to the main step will be equal in pitch to a sound raised by a semitone relative to the step that is two semitones lower.
Simply put, A-flat (A♭) and G-sharp (G♯) of the same octave sound identical. Similarly, within an octave, G-flat (G♭) and F-sharp (F♯), E-flat (E♭) and D-sharp (D♯), D-flat (D♭) and up to -sharp (С♯), etc. The phenomenon when sounds of the same height have different names and are indicated by different symbols is called anharmonicity of sounds.
For ease of perception, we have demonstrated this phenomenon on the example of steps (notes), between which there are 2 semitones. In other cases, when there is only 1 semitone between the main steps, this is less obvious. For example, F-flat (F♭) is pure E (E), and E-sharp (E♯) is pure F (F). Nevertheless, in the special literature on music theory, such designations as F-flat (F♭) and E-sharp (E♯) can also be found. You now know what they mean.
Today you have studied the basic physical properties of sound in general and the properties of musical sound in particular. You have dealt with the musical system and scale, scale steps, octaves, tones and semitones. You have also understood the note-octave system and are now ready to take a test on the material of the lesson, in which we have included the most important questions from a practical point of view.
Lesson comprehension test
If you want to test your knowledge on the topic of this lesson, you can take a short test consisting of several questions. Only 1 option can be correct for each question. After you select one of the options, the system automatically moves on to the next question. The points you receive are affected by the correctness of your answers and the time spent on passing. Please note that the questions are different each time, and the options are shuffled.
And now we turn to the analysis of musical notation.