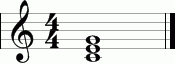
Musical sound and its properties

The play “4’33”” by John Cage is 4 minutes and 33 seconds of silence. With the exception of this work, all the others use sound.

Sound is to music what paint is to painting, the word is to the writer, and the brick is to the builder. Sound is the material of music. Should a musician know how sound works? Strictly speaking, no. After all, the builder may not know the properties of the material from which he builds. The fact that the building will collapse is not his problem, it is the problem of those who will live in this building.

At what frequency does the note C sound?

What properties of musical sound do we know?

Let’s take a string as an example.

Volume. It corresponds to the amplitude. The harder we hit the string, the wider the amplitude of its vibrations, the louder the sound will be.

duration. There are artificial computer tones that can sound for an arbitrarily long time, but usually the sound comes on at some point and stops at some point. With the help of sound duration, all rhythmic figures in music are lined up.

Height. We are used to saying that some notes sound higher, others lower. The pitch of the sound corresponds to the frequency of the vibration of the string. It is measured in hertz (Hz): one hertz is one time per second. Accordingly, if, for example, the frequency of sound is 100 Hz, this means that the string makes 100 vibrations per second.

If we open any description of the musical system, we will easily find that the frequency up to a small octave is 130,81 Hz, so in a second the string emitting to, makes 130,81 oscillations.

But this is not true.

Perfect String

So, let’s depict what we have just described in the picture (Fig. 1). For the time being, we discard the duration of the sound and denote only the pitch and loudness.

Here the red bar graphically represents our sound. The higher this bar, the louder the sound. The further to the right this column, the higher the sound. For example, two sounds in Fig. 2 will be the same volume, but the second (blue) will sound higher than the first (red).

Such a graph in science is called the amplitude-frequency response (AFC). It is customary to study all the features of sounds.

Now back to the string.

If the string vibrated as a whole (Fig. 3), then it would really make one sound, as shown in Fig. 1. This sound would have some volume, depending on the strength of the blow, and a well-defined frequency of oscillation, due to the tension and length of the string.

We can listen to the sound produced by such a vibration of the string.

* * *

Sounds poor, doesn’t it?

This is because, according to the laws of physics, the string does not vibrate quite like this.

All string players know that if you touch a string exactly in the middle, without even pressing it against the fretboard, and strike it, you can get a sound called flagolet. In this case, the form of vibrations of the string will look something like this (Fig. 4).

Here the string seems to be divided into two, and each of the halves sounds separately.

From physics it is known: the shorter the string, the faster it vibrates. In Fig. 4, each of the halves is two times shorter than the whole string. Accordingly, the frequency of the sound that we receive in this way will be twice as high.

The trick is that such a vibration of the string did not appear at the moment when we began to play the harmonic, it was also present in the “open” string. It’s just that when the string is open, such a vibration is more difficult to notice, and by placing a finger in the middle, we revealed it.

Figure 5 will help answer the question of how a string can simultaneously vibrate both as a whole and as two halves.

The string bends as a whole, and two half-waves oscillate on it like a kind of eight. The figure eight swinging on a swing is what the addition of two such types of vibrations is.

What happens to the sound when the string vibrates in this way?

It’s very simple: when a string vibrates as a whole, it emits a sound of a certain pitch, it is usually called the fundamental tone. And when two halves (eight) vibrate, we get a sound twice as high. These sounds play at the same time. On the frequency response, it will look like this (Fig. 6).

The darker column is the main tone arising from the vibration of the “whole” string, the lighter one is twice as high as the dark one, it is obtained from the vibration of the “eight”. Each bar on such a graph is called a harmonic. As a rule, higher harmonics sound quieter, so the second column is slightly lower than the first.

But the harmonics are not limited to the first two. In fact, besides the already intricate addition of a figure-eight with a swing, the string at the same time bends like three half-waves, like four, like five, and so on. (Fig. 7).

Accordingly, sounds are added to the first two harmonics, which in three, four, five, etc. times higher than the main tone. On the frequency response, this will give such a picture (Fig. 8).

Such a complex conglomerate is obtained when only one string sounds. It consists of all the harmonics from the first (which is called the fundamental) to the highest. All harmonics except the first are also called overtones, i.e. translated into Russian – “upper tones”.

We emphasize once again that this is the most basic idea of ​​​​sound, this is how all the strings in the world sound. In addition, with minor changes, all wind instruments give the same sound structure.

When we talk about sound, we mean exactly this construction:

SOUND = GROUND TONE + ALL MULTIPLE OVERTONS

It is on the basis of this structure that all its harmonic features are built in music. The properties of intervals, chords, tunings, and much more can be easily explained if you know the structure of sound.

But if all strings and all trumpets sound like this, why can we tell the piano from the violin, and the guitar from the flute?

Timbre

The question formulated above can be put even tougher, because professionals can even distinguish one guitar from another. Two instruments of the same shape, with the same strings, sound, and the person feels the difference. Agree, strange?

Before we resolve this oddity, let’s hear how the ideal string described in the previous paragraph would sound. Let’s sound the graph in Fig. 8.

* * *

It seems to be similar to the sound of real musical instruments, but something is missing.

Not enough “non-ideal”.

The fact is that in the world there are no two absolutely identical strings. Each string has its own characteristics, although microscopic, but affect how it sounds. Imperfections can be very diverse: thickness changes along the length of the string, different material densities, small braid defects, tension changes during vibration, etc. In addition, the sound changes depending on where we strike the string, the material properties of the instrument (such as susceptibility to moisture), how the instrument is positioned in relation to the listener, and much more, down to the geometry of the room.

What do these features do? They slightly modify the graph in Figure 8. The harmonics on it may turn out to be not quite multiple, slightly shifted to the right or left, the volume of different harmonics may change greatly, overtones located between the harmonics may appear (Fig. 9.).

Usually, all the nuances of sound are attributed to the vague concept of timbre.

Timbre seems to be a very convenient term for the peculiarities of an instrument’s sound. However, there are two problems with this term that I would like to point out.

The first problem is that if we define the timbre as we did above, then we distinguish the instruments by ear mainly not by it. As a rule, we catch the differences in the first fraction of a second of the sound. This period is usually called the attack, in which the sound just appears. The rest of the time, all sruns sound very similar. To verify this, let’s listen to a note on the piano, but with a “cut off” attack period.

* * *

Agree, it is quite difficult to recognize the well-known piano in this sound.

The second problem is that usually, when talking about sound, the main tone is singled out, and everything else is attributed to timbre, as if it is insignificant and does not play any role in musical constructions. However, this is not at all the case. It is necessary to distinguish individual features, such as overtones and deviations of harmonics, from the fundamental structure of sound. Individual characteristics really have little effect on musical constructions. But the fundamental structure – multiple harmonics, shown in Fig. 8. – is what determines all without exception harmony in music, regardless of eras, trends and styles.

We will talk about how this structure explains musical constructions next time.

Author – Roman Oleinikov Audio recordings – Ivan Soshinsky