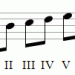
Circle of fifths in minor keys

How to play the same music in minor from different sounds?

This article is a continuation of the article ” Circle of Fifths of Major Keys “.

If you remember the circle of fifths of major keys (see the article ” The circle of fifths of major keys “), then it will not be difficult for you to deal with the circle of fifths of minor keys.

Recall the following:

• related keys are those that have 6 common sounds.
• parallel keys are those that have the same set of accidentals at the key, but one key is major and the other is minor.
• for parallel keys, the minor key tonic will be lower by a minor third of the major key tonic.

Circle of fifths in minor keys

The related keys of the minor, as well as the major, are located at a distance of a pure fifth from each other. In this regard, the keys of the minor form their own circle of fifths.

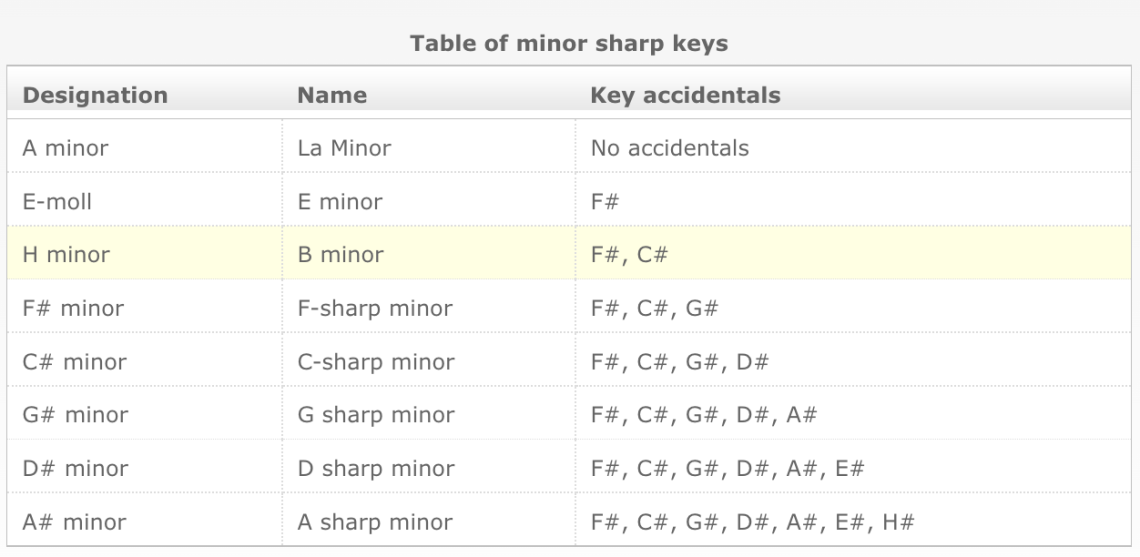
Knowing the circle of fifths of sharp major keys, we recalculate the tonics (we lower them by a minor third) and get the circle of fifths of sharp minor keys:

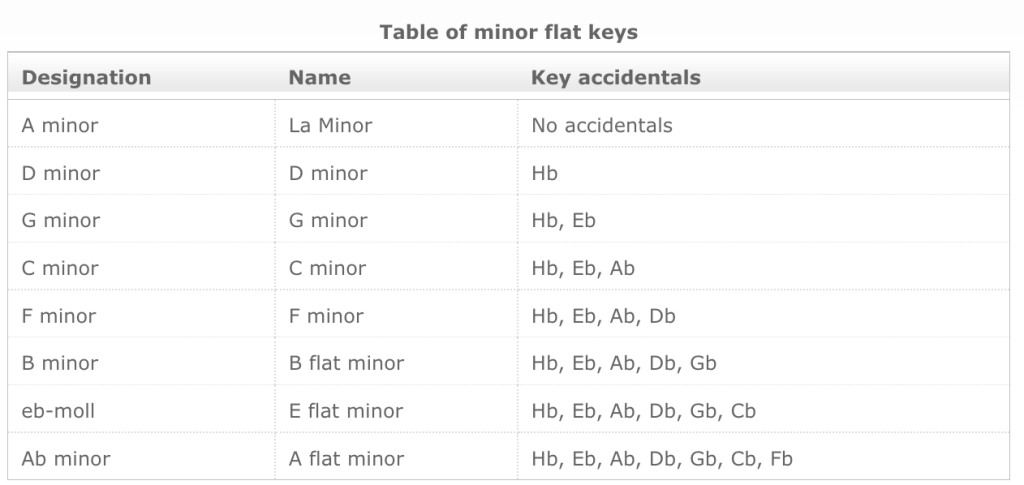
… and similarly the circle of fifths in flat minor keys:

Just like major, minor has three pairs of enharmonic equal keys:

1. G-sharp minor = A-flat minor
2. D-sharp minor = E-flat minor
3. A sharp minor = B flat minor

Like the major circle, the minor circle is “happy” to close, and in this it is helped by enharmonic equal sharp keys. Exactly the same as in the article ” Circle of Fifths of Major Keys “.

You can visually get acquainted with the circle of fifths of minor keys (we arranged minor keys on the inner circle, and major keys on the outer one; related keys are combined). 

Additionally

There are other ways to calculate the circle of fifths of minor keys. Let’s take a look at them.

1. If you remember well the circle of fifths of major keys, but the method described above for finding the tonic of a parallel minor key is inconvenient for some reason, then you can take the VI degree for the tonic. Example: looking for a parallel minor key for G-dur (G, A, H, C, D, E , F#). We take the sixth step as the tonic of the minor, this is the note E. That’s it, the calculation is finished! Since we found the tonic of exactly the parallel minor key, the accidentals of both keys coincide (in the found E-moll, like in G-dur, there is a sharp before the note F).

2. We do not start from the major circle, but calculate from scratch. All by analogy. We take a minor key without accidentals, this is A-moll. The fifth degree will be the tonic of the next (sharp) minor key. This is the note E. We put the accidental sign in front of the second step (note F) of the new key (E-moll). That’s it, the calculation is over.

Results

You got acquainted with the  circle of fifths of minor keys and learned how you can count the number of signs in different minor keys.