How to quickly find related tonalities of the second and third degrees?

Today we will do an interesting thing – we will learn to look for distant related tonalities, and to do this as quickly as we find “relatives” in the first degree.

First, let’s clarify one important detail. The fact is that some people prefer to use the Rimsky-Korsakov system, according to which there can be three degrees of relationship between tonalities, while others adhere to another system, according to which there are not three, but four of these degrees. So, we will take Rimsky-Korsakov’s system of family relations as a basis, since it is simpler, but we will not abandon the second system either and will discuss this topic separately at the end.

The difference between 3- and 4-level systems of kinship relations is that one of the groups of tonalities, namely the second, is simply divided into two or, if you like, absorbs two, which make up the 2nd and 3rd th degree in the 4-degree system. Let’s try to visualize what was said:

How to search for related tonalities of the second degree?

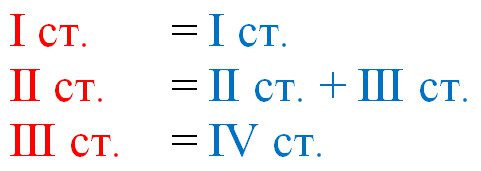
Here we need to find 12 keys in total. The very principle of where they come from is discussed in detail in the article “Degrees of relatedness of keys,” and now we will simply learn how to find them in major and minor.

Keys of the second degree of kinship for major

In a major scale, out of 12 keys, 8 must be major, the remaining 4 must be minor. Without further ado, we will refer to the steps of the original key. Perhaps it would be more correct to search by building intervals from the tonic, but it is easier to associatively link new tonalities to the steps of the original one.

So, to begin with, there are 4 minor keys, so we just remember the degrees: I (minor of the same name), V (minor dominant), VII (just remember – the seventh), VIIb (lowered seventh).

For example, for the key of C-dur (the letter designation of keys), these would be c-moll, g-moll, h-moll and b-moll.

Now there are 8 major keys and they are paired, now you will understand what is meant by the word “paired”. We tie them to the following steps: II, III, VI and VII. And everywhere it will be like this: a natural level and a lowered one, that is, two major keys for each degree (one without a flat tone, the other with a flat tone).

For example, for the same C major it will be: D-dur and Des-dur, E-dur and Es-dur, A-dur and As-dur, H-dur and B-dur. Everything is extremely simple, the main thing is to remember magic code – 2367 (composed of step numbers).

Keys of the second degree of kinship for minor

If our initial tonality is minor (for example, C minor), then for it 12 tonalities related to the second degree will be divided as follows: on the contrary, only 4 are major and the remaining 8 are minor.

The tonics of major keys will coincide with the following degrees (remember): I (major of the same name), II (simple second), IIb (second lowered), IV (major subdominant). For example, for C minor these will be the following “cousins”: C-dur, D-dur, Des-dur and F-dur.

There are eight minor keys and, pay attention, everything is very interesting here: their tonics occupy the same steps as the 8 major tonics for major: II, III, VI and VII in natural and reduced form. That is, related to C minor are such tonalities as d-moll and des-moll (a non-existent key, but everything is exactly as it is), e-moll and es-moll, a-moll and as-moll, h- moll and b-moll.

Interesting observation (can be skipped)

If we talk in general about cousins ​​for major and minor, then a number of interesting points emerge here:

• out of 24 (12+12) tonics for each case there are 9+9 (18) pieces that match tonally and differ only in modal inclination (including 8+8, which are associated with “code 2367” and the same 1+1);
• tones of the same name are relatives of the second degree in this system, and in the 4-degree system they generally turn out to be “second cousins”;
• the largest number of tonalities of the second degree of kinship are associated with the introductory degrees (on VII – 4 tonalities for major, on II – 4 tonalities for minor), with the stages on which diminished triads were built in the original tonality in the natural form of its mode, due to which these tonics are not included in the circle of relatives of the first degree (a kind of compensation occurs – multiplication by two to a subsequent degree);
• the related tonalities of the second degree included: for major – the tonality of a minor dominant, and for minor – the tonality of a major subdominant (and we remember about special cases in the circle of tonalities of the first degree – a minor subdominant in a harmonic major and a major dominant in a harmonic minor?).

Well, that’s enough, it’s time to move on and move on to the next, third degree of relationship, which characterizes the relationship between the most distant tonalities (they do not have a single common triad).

Third degree of relationship

Here, unlike the problem of the previous level, you don’t have to invent an elephant, you don’t have to invent a calculator or a bicycle. Everything has been known for a long time, everyone uses it successfully. I’ll tell you too!

Total five keys. In the same way, we will first consider the case if our initial key is major, and then the case if we are looking for missing relatives for a minor key.

Well, by the way, there are some things in common between these cases, there are even common tones (two of them). What this has in common is that the tonic of the two mentioned common tonalities are at triton distance from the original tonic. Moreover, we use this tonic twice – for major and minor keys.

So, if our initial key is major (the same C major, for example), then the note F-sharp is located at the distance of a tritone from its tonic. With F-sharp we make both major and minor. That is, two of the five keys are Fis-dur and fis-moll.

And then just miracles! From the resulting minor tritone key moving upward in perfect fifths. In total, we need to take three steps – we will get the three remaining keys: cis-moll, gis-moll and dis-moll.

If the initial key is minor (C minor for example), then we do almost the same: we build a tritone, and immediately get two keys (Fis-dur and fis-moll). And now, attention, from the major tritone key (that is, from Fis-dur) step down three fifths! We get: H-dur, E-dur and A-dur.

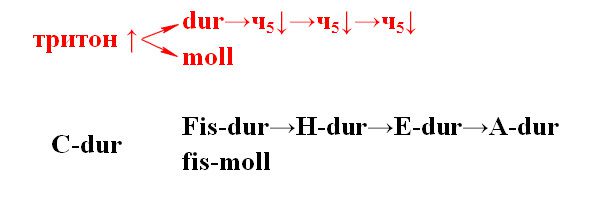
For those who adhere to the 4-degree system

It remains to figure out how to find related tonalities for those who prefer to distinguish four degrees instead of three. I’ll say right away that the fourth degree is the same third without changes. There are no problems with this.

But, as already mentioned, the second “by three” absorbs the second and third “by four”. And the second degree includes only 4 tonalities, and the third – 8. For yourself, you can still find 12 tonalities at once, and then exclude 4 tonalities of the second degree from them, so that you are left with 8 tonalities of the third degree.

How to find the tonality of the second degree “by four”?

This is the main feature of the Moscow system of tonal kinship. And, of course, everything here is logical and simple. It will be necessary to find double dominants and double subdominants (no matter how they are called correctly).

In major, we are looking for the tonality of the double dominant (II degree with a major triad on it) and its parallel, as well as the tonality of the double subdominant (VII low with a major triad on it) and its parallel. Examples for C major are D-dur||h-moll and B-dur||g-moll. All!

In minor we do the same thing, only we leave everything that we find minor (that is, the double dominant is not like that – DD, but like dd – natural, about the subdominant – similarly). We add parallels to what we found and get tonalities of the second degree of kinship for C minor: d-moll||F-dur and b-moll||Des-dur. Everything ingenious is simple!