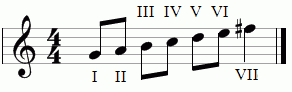Simple and compound intervals
Contents
There are only 15 intervals in music. Eight of them (from prima to octave) are called simple, they are most often found in musical plays and songs. The remaining seven are compound intervals. They are composite because they are, as it were, composed of two simple intervals – an octave and some other interval, which is added to this octave.
We have already talked a lot about simple intervals before, and today we will deal with the second half of the intervals, which most students of music schools do not know about or simply forget about their existence.
Names of compound intervals
Compound intervals, just like simple ones, are denoted by numbers (from 9 to 15) and numerals in Latin are also used for their names:
9 – nona (interval of 9 steps) 10 – decima (10 steps) 11 – undecima (11 steps) 12 – duodecyma (12 steps) 13 – terzdecima (13 steps) 14 – quarterdecima (14 steps) 15 – quintdecima (15 steps)
Any interval has a quantitative and qualitative value. And in this case, the numerical designation shows the coverage of the interval, that is, the number of steps that need to be passed from the lower sound to the upper one. Due to the qualitative value, the intervals are divided into pure, small, large, enlarged and reduced. And this also fully applies to compound intervals.
What are compound intervals?
Compound intervals are always wider than an octave, so the first element is a pure octave. Some simple interval from a second to another octave is built on top of it. What is the result?
Nona (9) is an octave + second (8+2). And since a second can be small or large, nona also comes in varieties. For example: DO-RE (everything through the octave) is a big nona, since we added a big second to the pure octave, and the notes DO and D-FLAT, respectively, form a small nona. Here are examples of large and small nons from different sounds:

to children (10) is an octave and a third (8 + 3). Decima can also be large and small, depending on which third was added to the octave. For example: RE-FA – small decima, RE and FA-SHARP – large. Examples of different decims built from all the basic sounds:

Undecima(11) is an octave + quart (8 + 4). The quart is most often pure, so the undecima is also pure. If desired, you can, of course, make both reduced and enlarged undecima. For example: DO-FA – pure, DO and FA-SHARP – increased, DO and F-FLAT – reduced undecima. Examples of pure undecime from all “white keys”:

Duodecima (12) is an octave + fifth (8 + 5). Duodecymes are often clean. Examples:

Tercdecima (13) is an octave + sixth (8 + 6). Since sixths exist large and small, terdecimals are exactly the same. For example: RE-SI is a large third decimal, and MI-DO is a small one. More examples:

Quartdecima (14) is an octave and a seventh (8 + 7). Similarly, there are large and small. In the musical examples, for convenience, the lower voice had to be written in the bass clef:

Quintdecima (15) – these are two octaves, an octave + one more octave (8 + 8). examples:

And we will show one more musical example: we will collect in it all the compound intervals built from the notes DO and PE. It will be clearly seen how with an increase in the number of the interval, the interval itself gradually expands, and its sounds gradually move away from each other.

Compound interval table
For greater clarity, let’s compile a table of compound intervals, in which it will be clearly seen what their varieties are possible, how they are formed and how they are designated.
| Interval | Composition | Types | Notation |
| nona | octave + second | small | m.9 |
| great | p.9 | ||
| decima | octave + third | small | m.10 |
| great | p.10 | ||
| undecima | octave + quart | net | part 11 |
| duodecima | octave + fifth | net | part 12 |
| terdecima | octave + sixth | small | m.13 |
| great | p.13 | ||
| quartets | octave + seventh | small | m.14 |
| great | p.14 | ||
| quintdecima | octave + octave | net | part 15 |
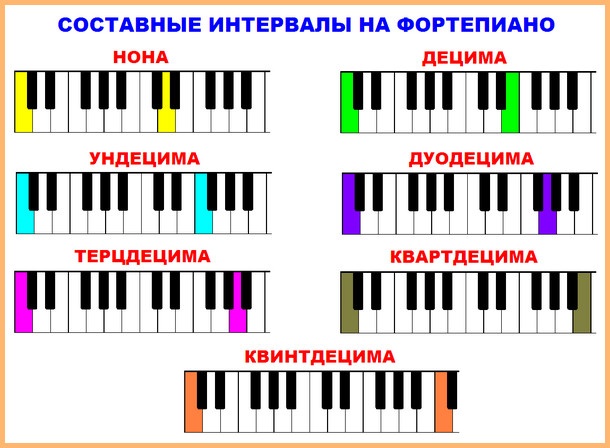
Compound intervals on the piano
When you are learning, it is useful not only to build intervals in notes, but also to play on the piano. As an exercise, play the compound intervals from the note C on the piano and listen to how they sound. You can still play without highlighting the varieties, the main thing is to remember the names and the very principle of construction.
Well, how? Got it? If yes, then great! In the next issues we will talk about how harmonic and melodic intervals differ and how to distinguish them by ear. In order not to miss anything, join our Facebook group.