A way to see musical harmony

When we talk about melody, we have a very good helper – the stave.

Looking at this picture, even a person who is not familiar with musical literacy can easily determine when the melody goes up, when it goes down, when this movement is smooth, and when it jumps. We literally see which notes are melodically closer to each other and which are farther.

But in the field of harmony, everything seems to be completely different: close notes, for example, to и ре sound quite dissonant together, and more distant ones, for example, to и E – much more melodious. Between the completely consonant fourth and fifth is a completely dissonant tritone. The logic of harmony turns out to be somehow completely “non-linear”.

Is it possible to pick up such a visual image, looking at which, we can easily determine how “harmonically” two notes are close to each other?

 “Valences” of the sound

Let us recall once again how the sound is arranged (Fig. 1).

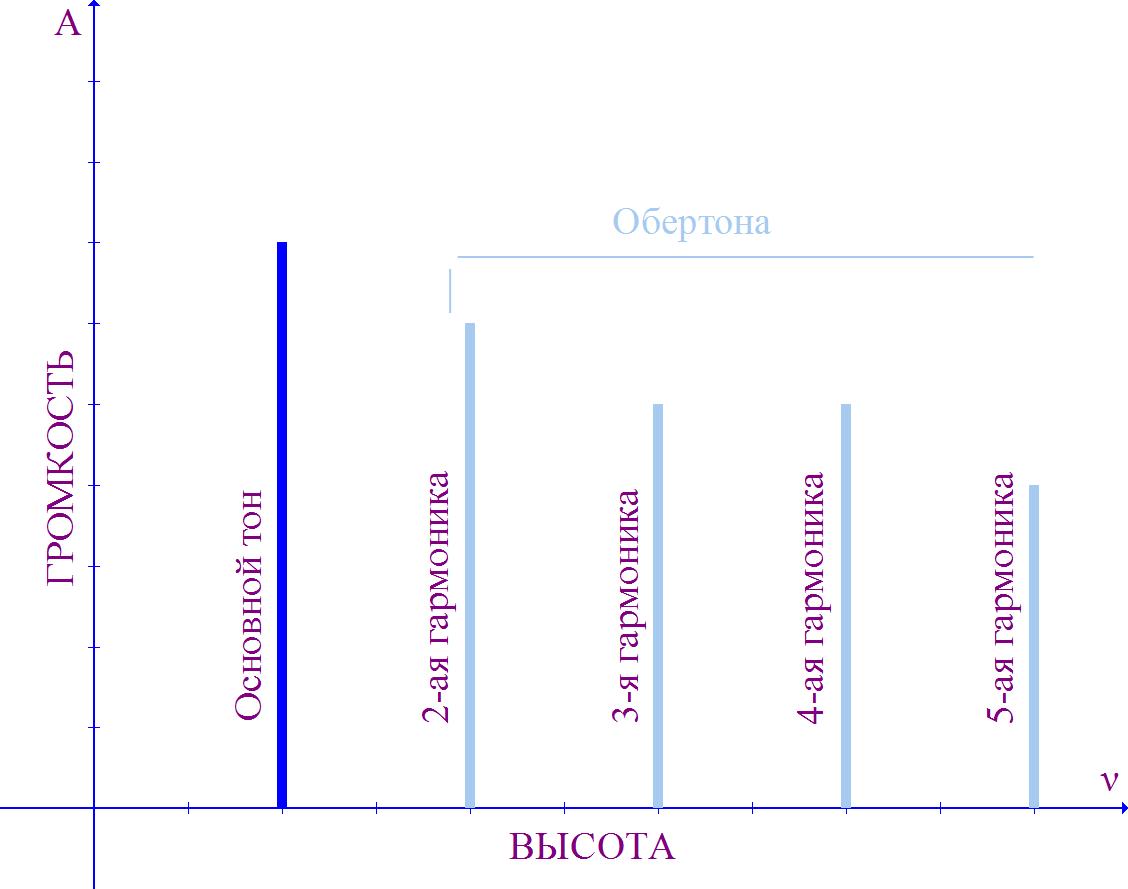
Each vertical line on the graph represents the harmonics of the sound. All of them are multiples of the fundamental tone, that is, their frequencies are 2, 3, 4 … (and so on) times greater than the frequency of the fundamental tone. Each harmonic is a so-called monochrome sound, that is, the sound in which there is one single frequency of oscillation.

When we play just one note, we are actually producing a huge number of monochrome sounds. For example, if a note is played for small octave, whose fundamental frequency is 220 Hz, at the same time monochromatic sounds at frequencies of 440 Hz, 660 Hz, 880 Hz and so on (about 90 sounds within the human auditory range) sound.

Knowing such a structure of harmonics, let’s try to figure out how to connect two sounds in the simplest way.

The first, simplest, way is to take two sounds whose frequencies differ by exactly 2 times. Let’s see how it looks in terms of harmonics, placing the sounds one under the other (Fig. 2).

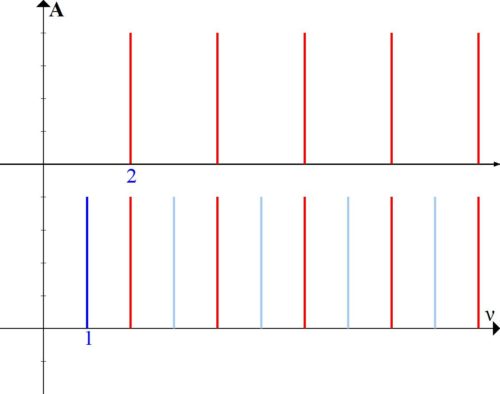
We see that in this combination, the sounds actually have the same every second harmonic (coinciding harmonics are indicated in red). The two sounds have a lot in common – 50%. They will be “harmonically” very close to each other.

The combination of two sounds, as you know, is called an interval. The interval shown in Figure 2 is called octave.

It is worth mentioning separately that such an interval “coincided” with the octave is not accidental. In fact, historically, the process, of course, was the opposite: at first they heard that two such sounds sounded together very smoothly and harmoniously, fixed the method of constructing such an interval, and then called it an “octave”. The method of construction is primary, and the name is secondary.

The next way of communication is to take two sounds, the frequencies of which differ by 3 times (Fig. 3).

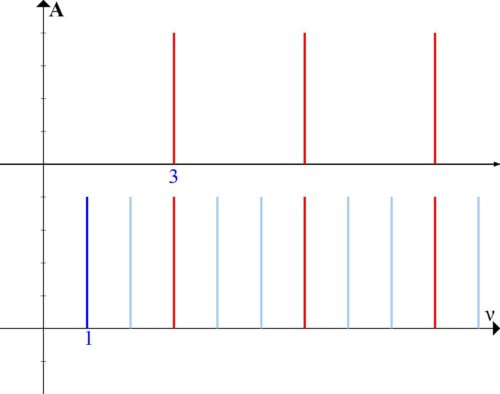
We see that here the two sounds have a lot in common – every third harmonic. These two sounds will also be very close, and the interval, accordingly, will be consonant. Using the formula from the previous note, you can even calculate that the measure of frequency consonance of such an interval is 33,3%.

This interval is called duodecima or a fifth through an octave.

And finally, the third way of communication, which is used in modern music, is to take two sounds with a chatot difference of 5 times (Fig. 4).

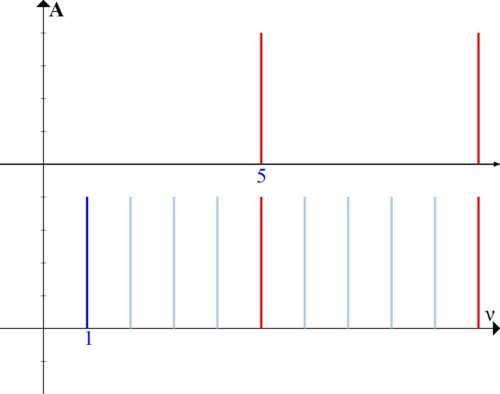
Such an interval does not even have its own name, it can only be called a third after two octaves, however, as we see, this combination also has a rather high measure of consonance – every fifth harmonic coincides.

So, we have three simple connections between notes – an octave, a duodecim and a third through two octaves. We will call these intervals basic. Let’s hear how they sound.

Audio 1. Octave

.

Audio 2. Duodecima

.

Audio 3. Third through an octave

.

Quite consonant indeed. In each interval, the top sound actually consists of the harmonics of the bottom and does not add any new monochrome sound to its sound. For comparison, let’s listen to how one note sounds to and four notes: to, an octave sound, a duodecimal sound, and a sound that is higher by a third every two octaves.

Audio 4. Sound to

.

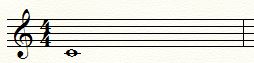
Audio 5. Chord: C-C-S-E

.

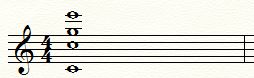
As we hear, the difference is small, just a few harmonics of the original sound are “amplified”.

But back to basic intervals.

Multiplicity space

If we select some note (for example, to), then the notes located one basic step away from it will be the most “harmonically” closest to it. The closest will be the octave, a little further the duodecimal, and behind them – the third through two octaves.

In addition, for each base interval, we can take several steps. For example, we can build an octave sound, and then take another octave step from it. To do this, the frequency of the original sound must be multiplied by 2 (we get an octave sound), and then multiplied by 2 again (we get an octave from an octave). The result is a sound that is 4 times higher than the original. In the figure, it will look like this (Fig. 5).

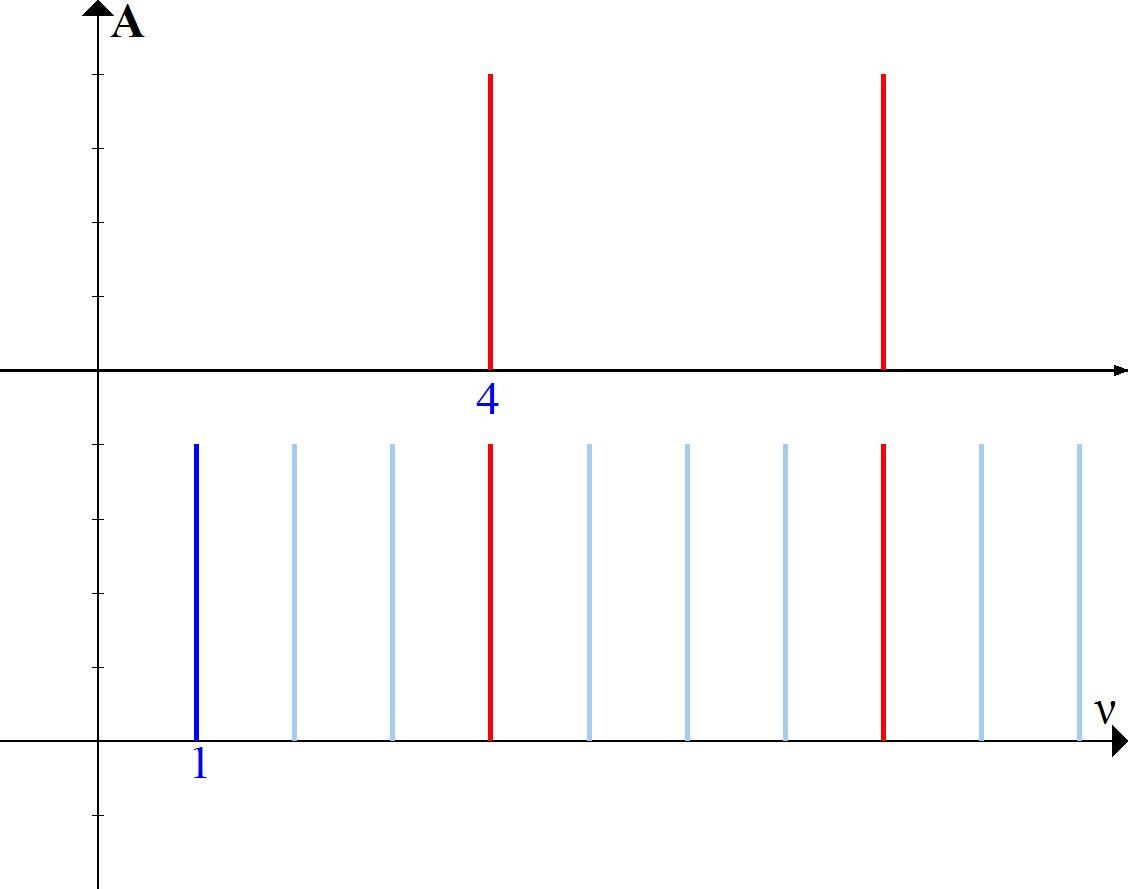
It can be seen that with each next step, the sounds have less and less in common. We are moving further and further away from consonance.

By the way, here we will analyze why we took multiplication by 2, 3 and 5 as basic intervals, and skipped multiplication by 4. Multiplying by 4 is not a base interval, because we can get it using already existing base intervals. In this case, multiplying by 4 is two octave steps.

The situation is different with base intervals: it is impossible to obtain them from other base intervals. It is impossible, by multiplying 2 and 3, to get neither the number 5 itself, nor any of its powers. In a sense, the base intervals are “perpendicular” to each other.

Let’s try to picture it.

Let’s draw three perpendicular axes (Fig. 6). For each of them, we will plot the number of steps for each basic interval: on the axis directed at us, the number of octave steps, on the horizontal axis, duodecimal steps, and on the vertical axis, tertian steps.

Such a chart will be called space of multiplicities.

Considering three-dimensional space on a plane is rather inconvenient, but we will try.

On the axis, which is directed towards us, we set aside octaves. Since all notes located an octave apart are named the same, this axis will be the most uninteresting for us. But the plane, which is formed by the duodecimal (fifth) and tertian axes, we will take a closer look (Fig. 7).

Here the notes are indicated with sharps, if necessary, they can be designated as enharmonic (that is, equal in sound) with flats.

Let’s repeat once again how this plane is built.

Having chosen any note, one step to the right of it, we place the note that is one duodecime higher, to the left – one duodecim lower. Taking two steps to the right, we get duodecyma from duodecyma. For example, taking two duodecimal steps from the note to, we get a note ре.

One step along the vertical axis is a third through two octaves. When we take steps up along the axis, this is a third through two octaves up, when we take steps down, this interval is laid down.

You can step from any note and in any direction.

Let’s see how this scheme works.

We choose a note. Making steps from notes, we get a note less and less consonant with the original. Accordingly, the farther the notes are from each other in this space, the less consonant interval they form. The closest notes are neighbors along the octave axis (which, as it were, is directed at us), a little further – neighbors along the duodecimal, and even further – along the terts.

For example, to get from the note to up to a note yours, we need to take one duodecimal step (we get salt), and then one terts, respectively, the resulting interval do-si will be less consonant than duodecime or third.

If the “distances” in the PC are equal, then the consonances of the corresponding intervals will be equal. The only thing we must not forget about the octave axis, invisibly present in all constructions.

It is this diagram that shows how close the notes are to each other “harmonically”. It is on this scheme that it makes sense to consider all harmonic constructions.

You can read more about how to do this in “Building Musical Systems”Well, we’ll talk about that next time.

Author – Roman Oleinikov