Inversion of intervals or magic in solfeggio lessons

Inversion of intervals is the transformation of one interval into another by rearranging the upper and lower sounds. As you know, the lower sound of an interval is called its base, and the upper sound is called the top.

And, if you swap the top and bottom, or, in other words, simply turn the interval upside down, then the result will be a new interval, which will be the inversion of the first, original musical interval.

How are interval inversions performed?

First, we will analyze the manipulations only with simple intervals. The conversion is performed by moving the lower sound, that is, the base, up a pure octave, or moving the lower sound of the interval, that is, the top, down an octave. The result will be the same. Only one of the sounds moves, the second sound remains in its place, you do not need to touch it.

For example, let’s take a big third “do-mi” and turn it in any way. First, we move the “do” base up an octave, we get the “mi-do” interval – a small sixth. Then let’s try to do the opposite and move the upper sound “mi” down an octave, as a result we also get a small sixth “mi-do”. In the picture, the sound that remains in place is highlighted in yellow, and the one that moves an octave is highlighted in lilac.

Another example: the interval “re-la” is given (this is a pure fifth, since there are five steps between sounds, and the qualitative value is three and a half tones). Let’s try to reverse this interval. We transfer “re” above – we get “la-re”; or we transfer “la” below and also get “la-re”. In both cases, the pure fifth turned into a pure fourth.

By the way, by reverse actions, you can return to the original intervals. So, the sixth “mi-do” can be turned into the third “do-mi”, from which we first started, but the fourth “la-re” can easily be turned back into the fifth “re-la”.

What does it say? This suggests that there is some connection between different intervals, and that there are pairs of mutually reversible intervals. These interesting observations formed the basis of the laws of interval inversions.

Laws of interval reversal

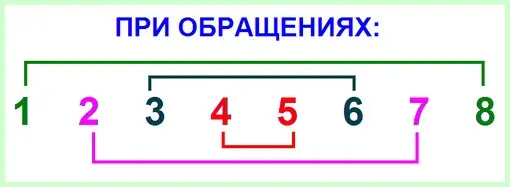
We know that any interval has two dimensions: a quantitative and a qualitative value. The first is expressed in how many steps this or that interval covers, is indicated by a number, and the name of the interval depends on it (prima, second, third, and others). The second indicates how many tones or semitones are in the interval. And, thanks to it, the intervals have additional clarifying names from the words “pure”, “small”, “large”, “increased” or “reduced”. It should be noted that both parameters of the interval change when accessed – both the step indicator and the tone.

There are only two laws.

Rule 1. When inverted, pure intervals remain pure, small ones turn into large ones, and large ones, on the contrary, into small ones, reduced intervals become increased, and increased intervals, in turn, are reduced.

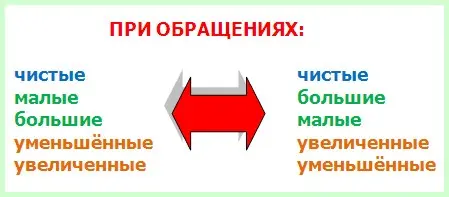
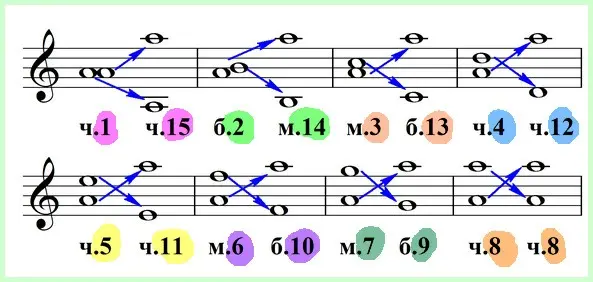
Rule 2. Prims turn into octaves, and octaves into prims; seconds turn into sevenths, and sevenths into seconds; thirds become sixths, and sixths become thirds, quarts become fifths, and fifths, respectively, into fourths.

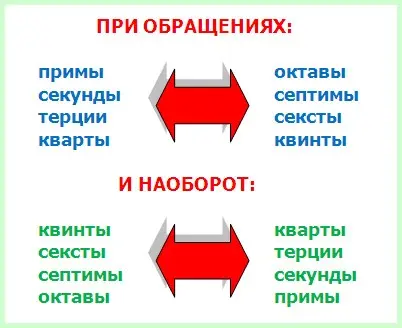
The sum of designations of mutually inverting simple intervals is equal to nine. For example, prima is indicated by the number 1, octave by the number 8. 1+8=9. Second – 2, seventh – 7, 2+7=9. Thirds – 3, sixths – 6, 3+6=9. Quarts – 4, fifths – 5, together again it turns out 9. And, if you suddenly forgot who goes where, then simply subtract the numerical designation of the interval given to you from nine.

Let’s see how these laws work in practice. Several intervals are given: a pure prima from D, a minor third from mi, a major second from C-sharp, a diminished seventh from F-sharp, an augmented fourth from D. Let’s reverse them and see the changes.

So, after the conversion, the pure prima from D turned into a pure octave: thus, two points are confirmed: firstly, pure intervals remain pure even after the conversion, and, secondly, the prima has become an octave. Further, the small third “mi-sol” after the conversion appeared as a large sixth “sol-mi”, which again confirms the laws we have already formulated: the small grew into a large, the third became a sixth. The following example: the big second “C-sharp and D-sharp” turned into a small seventh of the same sounds (small – into a large, second – into a seventh). Similarly in other cases: the reduced becomes increased and vice versa.

Test yourself!

We suggest a little practice to better consolidate the topic.

EXERCISE: Given a series of intervals, you need to determine what these intervals are, then mentally (or in writing, if it is difficult so immediately) to turn them and say what they will turn into after the conversion.

Focuses with compound intervals

Compound intervals can also participate in circulation. Recall that intervals that are wider than an octave, that is, nones, decims, undecims, and others, are called composite.

To get a compound interval when inverted from a simple interval, you need to move both the top and the bottom at the same time. Moreover, the base is an octave up, and the top is an octave down.

For example, let’s take a major third “do-mi”, move the base “do” an octave higher, and the top “mi”, respectively, an octave lower. As a result of this double movement, we got a wide interval “mi-do”, a sixth through an octave, or, to be more precise, a small third decimal.

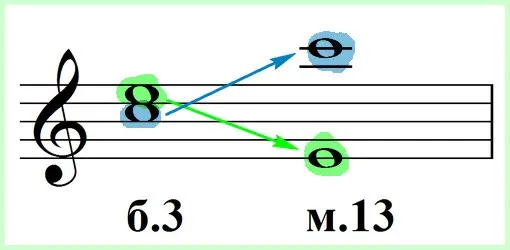
In a similar way, other simple intervals can be turned into compound intervals, and vice versa, a simple interval can be obtained from a compound interval if its top is lowered by an octave and its base is raised.

What rules will be followed? The sum of the designations of two mutually invertible intervals will be equal to sixteen. So:

• Prima turns into quintdecima (1+15=16);
• A second turns into a quarterdecimum (2+14=16);
• The third passes into the third decima (3+13=16);
• The quart becomes the duodecima (4+12=16);
• Quinta reincarnates into undecima (5+11=16);
• Sexta turns into a decima (6+10=16);
• Septima appears as nona (7+9=16);
• These things don’t work with an octave, it turns into itself and therefore compound intervals have nothing to do with it, although there are beautiful numbers in this case too (8+8=16).

Applying interval inversions

You should not think that the inversion of intervals, studied in such detail in the school solfeggio course, have no practical application. On the contrary, it is a very important and necessary thing.

The practical scope of inversions is not only related to understanding how certain intervals arose (yes, historically, some intervals were discovered by inversion). In the theoretical field, inversions are very helpful, for example, in memorizing tritones or characteristic intervals studied in high school and college, in understanding the structure of certain chords.

If we take the creative area, then appeals are widely used in composing music, and sometimes we don’t even notice them. Listen, for example, to a piece of a beautiful melody in a romantic spirit, it is all built on ascending intonations of thirds and sixths.

By the way, you can also easily try to compose something similar. Even if we take the same thirds and sixths, only in a descending intonation:

PS Dear friends! On that note, we conclude today’s episode. If you have any more questions about spacing inversions, then please ask them in the comments to this article.

P.P.S For the final assimilation of this topic, we suggest you watch a funny video from a wonderful solfeggio teacher of our days, Anna Naumova.