Increased and decreased intervals: how to build them?
Contents
You know that intervals are pure, small and large, but they can also be increased and decreased, and in addition – doubled and doubled. But how to get such intervals, how to construct and define them? This is what we will talk about today.
Previous important topics:
WHAT ARE INTERVALS AND WHAT THEY ARE – READ HERE
QUANTITATIVE AND QUALITATIVE VALUE OF THE INTERVAL – READ HERE
What are extended and decreased intervals?
Extended intervals are obtained by adding a semitone to a pure or large interval, that is, if the qualitative value is slightly changed. You can increase all intervals – from prima to octaves. The abbreviated way of designating such intervals is “uv”.
Let’s compare in the following table the number of tones and semitones in ordinary intervals, that is, pure and large, and in enlarged ones.
Table – Qualitative value of clean, large and enlarged intervals
| original interval | How many tones | Increased interval | How many tones |
| part 1 | 0 item | uv.1 | 0,5 item |
| p.2 | 1 item | uv.2 | 1,5 item |
| p.3 | 2 item | uv.3 | 2,5 item |
| part 4 | 2,5 item | uv.4 | 3 item |
| part 5 | 3,5 item | uv.5 | 4 item |
| p.6 | 4,5 item | uv.6 | 5 item |
| p.7 | 5,5 item | uv.7 | 6 item |
| part 8 | 6 item | uv.8 | 6,5 item |
Reduced intervals, on the contrary, arise when pure and small intervals are narrowed, that is, when their qualitative value decreases by half a tone. Decrease any interval, except pure prima. The fact is that in the prime there are zero tones, from which you can’t subtract anything else. Abbreviated reduced intervals are written as “mind”.
For greater clarity, we will also build a table with the values of the qualitative quantity for the increased intervals and their prototypes: pure and small.
Table – Qualitative value of pure, small and reduced intervals
| original interval | How many tones | Reduced interval | How many tones |
| part 1 | 0 item | no | no |
| m.2 | 0,5 item | mind. 2 | 0 item |
| m.3 | 1,5 item | mind. 3 | 1 item |
| part 4 | 2,5 item | mind. 4 | 2 item |
| part 5 | 3,5 item | mind. 5 | 3 item |
| m.6 | 4 item | mind. 6 | 3,5 item |
| m.7 | 5 item | mind. 7 | 4,5 item |
| part 8 | 6 item | mind. 8 | 5,5 item |
How to build increased and decreased intervals?
To build any enlarged and reduced interval, the easiest way is to imagine its “source”, that is, a large, small or pure interval, and simply change something in it (narrow it or expand it).
How can the interval be extended? To do this, you can either raise its upper sound with a sharp by half a tone, or lower its lower sound with a flat. This is very clearly seen if we take the interval on the piano keyboard. Let’s take a pure fifth of D-LA as an example and see how it can be increased:
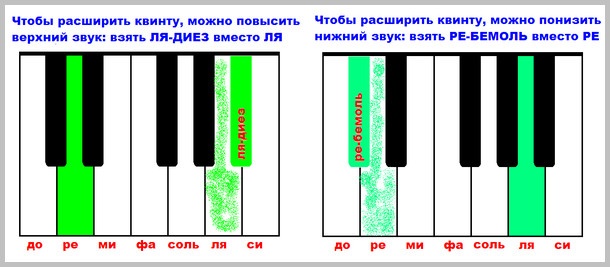
What are the results? The augmented fifth from the original pure is either D and A SHARP, or D FLAT and A, depending on which sound we have chosen to change. By the way, if we change both sounds at once, then the fifth will become doubled, that is, it will expand by two semitones at once. See how these results look in music notation:

How can you narrow the interval? You need to do the opposite, that is, turn it inward. To do this, we either lower the upper sound by half a step, or, if we manipulate the lower sound, we increase it, raise it a little. As an example, consider the same fifth of RE-LA and try to narrow it, that is, reduce it.
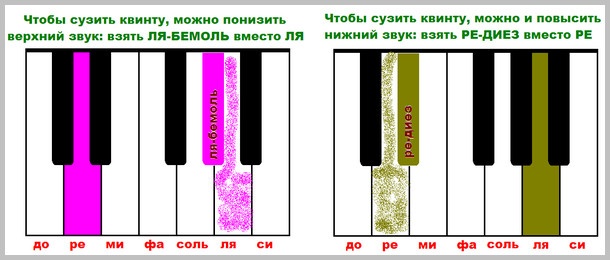
What have we achieved? There was a pure fifth of D-LA, we got two options for a reduced fifth: RE and A-FLAT, D-SHARP and LA. If you change both sounds of a fifth at once, then a twice reduced fifth of D-SHARP and A-FLAT will come out. Let’s look at a musical example:

See what you can do with other intervals. Now you have four musical examples. Compare them and observe how others are obtained from some intervals by manipulating the upper sound – it goes up and down by a semitone.
Example 1. Pure and large intervals from PE, built up

Example 2 Extended intervals from PE up

Example 3. Pure and small intervals from PE built up

Example 4 Reduced intervals from PE up

Anharmonicity of intervals
What enharmonism? it equality of elements of music in sound, but inequality in title and recording. A simple example of anharmonicity is F-SHARN and G-FLAT. It sounds the same, but the names are different, and they are also written differently. So, intervals can also be enharmonic equal, for example, a minor third and an augmented second.

Why are we talking about this at all? When you looked at the table with the number of tones at the beginning of the article, when you later looked at our examples, you probably wondered: “How can this be half a tone in an increased prime, because half a tone is in a small second?” or “What kind of D-LA-SHARP, write D-FAT and you get a normal small sixth, why all these increased fifths?”. Were there such thoughts? Admit you were. These are just examples of anharmonicity of intervals.
In enharmonic equal intervals, the qualitative value, that is, the number of tones and semitones, is the same, but the quantitative value (number of steps) is different, which is why they are made up of different sounds and are called differently.
Let’s see more examples of anharmonisms. Take the same intervals from PE. An augmented second sounds like a minor third, a major third equals a diminished fourth, an augmented fourth is the same as a diminished fifth, and so on.

Building increased and decreased intervals is not difficult for someone who has learned well how to build regular intervals. Therefore, if you have gaps in practice, then urgently eliminate them. That’s all. In the next issues we will talk about consonances and dissonances, about how harmonic and melodic intervals sound. We are waiting for your visit!