The strongest dissonance

What is dissonance? In simple terms, it is a discordant, unpleasant combination of various sounds. Why are such combinations present among intervals and chords? Where did they come from and why are they needed?

Journey of Odysseus

As we found out in the previous note, during the Antiquity, the Pythagorean system dominated. In it, all the sounds of the system are obtained by simply dividing the string into 2 or 3 equal parts. The halving simply shifts the sound by an octave. But division by three gives rise to new notes.

A legitimate question arises: when should we stop this division? From each new note, dividing the string by 3, we can get another one. Thus, we can get 1000 or 100000 sounds in the music system. Where should we stop?

When Odysseus, the hero of an ancient Greek poem, returned to his Ithaca, many obstacles awaited him on the way. And each of them delayed his journey until he found how to deal with it.

On the way to the development of musical systems, too, there were obstacles. For some time they slowed down the process of the appearance of new notes, then they overcame them and sailed on, where they met the next obstacle. These barriers were dissonances.

Let’s try to understand what dissonance is.

We can get an exact definition of this phenomenon when we understand the physical structure of sound. But now we do not need accuracy, it is enough for us to explain it in simple words.

So we have a string. We can divide it into 2 or 3 parts. Thus we get the octave and duodecim. An octave sounds more consonant, and this is understandable – division by 2 is easier than division by 3. In turn, a duodecima will sound more consonant than a string divided into 5 parts (such a division will give a third after two octaves), because division by 3 is simpler, than dividing by 5.

Now let’s remember how, for example, a fifth was built. We divided the string into 3 parts, and then increased the resulting length by 2 times (Fig. 1).

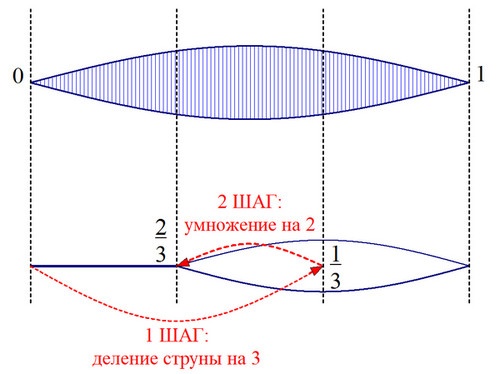
As you can see, to build a fifth, we need to take not one, but two steps, and, therefore, a fifth will sound less consonant than an octave or duodecime. With each step, we seem to be moving further and further away from the original note.

We can formulate a simple rule for determining consonance:

the fewer steps we take, and the simpler these steps themselves, the more consonant the interval will be.

Let’s get back to construction.

So, people have chosen the first sound (for convenience, we will assume that this to, although the ancient Greeks themselves did not call it that) and began to build other notes by dividing or multiplying the length of the string by 3.

First received two sounds, which to to were the closest F и salt (pic 2). Salt is obtained if the length of the string is reduced by 3 times, and F – on the contrary, if it is increased by 3 times.

The π index will still mean that we are talking about the notes of the Pythagorean system.

If you move these notes to the same octave where the note is located to, then the intervals before them will be called a fourth (do-fa) and a fifth (do-sol). These are two very remarkable intervals. During the transition from the Pythagorean system to the natural one, when almost all intervals changed, the construction of the fourth and fifth remained unchanged. The formation of the tonality went with the most direct participation of these notes, it was on them that the dominant and subdominant were built. These intervals turned out to be so consonant that they dominated music until the era of romanticism, and even after they were assigned a very significant role.

But we digress from the dissonances. The construction did not stop on these three notes. Sruna continued to be divided into 3 parts and duodecyma after duodecyma to receive new and new sounds.

The first obstacle arose at the fifth step, when to (original note) re, fa, sol, la note added E (pic 3).

Between notes E и F an interval was formed that seemed terribly dissonant to the people of that time. This interval was a small second.

Small second mi-fa – harmonic

*****

Having met this interval, we decided what to include E the system is no longer worth it, you need to stop at 5 notes. So the first system turned out to be 5-note, it was called pentatonic. All intervals in it are very consonant. The pentatonic scale can still be found in folk music. Sometimes, as a special paint, it is also present in the classics.

Over time, people got used to the sound of a small second and realized that if you use it moderately and to the point, then you can live with it. And the next obstacle was step number 7 (Fig. 4).

The new note turned out to be so dissonant that they even decided not to give it its own name, but called it F sharp (denoted f#). Actually sharp and means the interval that was formed between these two notes: F и F sharp. It sounds like this:

The interval F and F-sharp is harmonic

*****

If we do not go “beyond the sharp”, then we get a 7-note system – diatonic. Most classical and modern musical systems are 7-step, that is, they inherit the Pythagorean diatonic in this respect.

Despite such a huge importance of diatonicism, Odysseus sailed on. Having overcome the obstacle in the form of a sharp, he saw an open space in which you can type as many as 12 notes into the system. But the 13th formed a terrible dissonance – Pythagorean comm.

Pythagorean comma

*****

Perhaps we can say that the comma was Scylla and Charybdis rolled into one. It took not years or even centuries to overcome this obstacle. Only a couple of thousand years later, in the 12th century AD, did musicians seriously turn to microchromatic systems, which contain more than XNUMX notes. Of course, over the course of these centuries, individual attempts were made to add a few more sounds to the octave, but these attempts were so timid that, unfortunately, one cannot speak of their significant contribution to musical culture.

Can the attempts of the XNUMXth century be considered fully successful? Have microchromatic systems come into musical use? Let us return to this question, but before that we will consider a few more dissonances, no longer from the Pythagorean system.

wolf and devil

When we cited dissonant intervals from the Pythagorean system, we were a little cunning. That is, there were both a small second and a sharp, but then they heard them a little differently.

The fact is that the music of antiquity was predominantly of a monodic warehouse. Simply put, only one note sounded at a time, and the vertical – the simultaneous combination of several sounds – was almost never used. Therefore, ancient music lovers, as a rule, heard both a small second and a sharp sharp like this:

Minor second mi-fa – melodic

*****

Semitone F and F sharp – melodic

*****

But with the development of the vertical, harmonic (vertical) intervals, including dissonant ones, sounded to the fullest.

The first in this series should be called triton.

This is what a tritone sounds like

*****

It is called a tritone, not because it looks like an amphibian, but because it has exactly three whole tones from the lower sound to the upper one (that is, six semitones, six piano keys). Interestingly, in Latin it is also called tritonus.

This interval can be constructed both in the Pythagorean system and in natural. And here and there it will sound dissonant.

To build it in the Pythagorean system, you will have to divide the string into 3 parts 6 times, and then double the resulting length 10 times. It turns out that the length of the string will be expressed as a fraction 729/1024. Needless to say, with so many steps, there is no need to talk about consonance.

In natural tuning, the situation is slightly better. A natural tritone can be obtained as follows: divide the length of the string by 3 twice (i.e., divide by 9), then divide by another 5 (total divide by 45 parts), and then double it 5 times. As a result, the length of the string will be 32/45, which, although a little simpler, does not promise consonance.

According to rumors in the Middle Ages, this interval was called “the devil in music.”

But another consonance turned out to be more important for the development of music – wolf fifth.

Wolf Quint

*****

Where does this interval come from? Why is it needed?

Suppose we type sounds in a natural system from a note to. It has a note ре it turns out if we divide the rune into 3 parts twice (we take two duodecimal steps forward). A note A formed a little differently: to obtain it, we need to increase the string 3 times (take one step back along the duodecims), and then divide the resulting string length into 5 parts (that is, take the natural third, which just did not exist in the Pythagorean system). As a result, between the lengths of the strings of notes ре и A we get not a simple ratio of 2/3 (pure fifth), but a ratio of 40/27 (wolf fifth). As we see from the relation, this consonance cannot be consonant.

Why don’t we take a note A, which would be a pure fifth of ре? The fact is that then we will have two notes A – “quint from re” and “natural”. But with the “quint” A will have the same problems as ре – she will need her fifth, and we will already have two notes E.

And this process is unstoppable. In place of one head of the hydra, two appear. By solving one problem, we create a new one.

The solution to the problem of wolf fifths turned out to be radical. They created an evenly tempered system, where the “fifth” A and “natural” were replaced by one note – tempered A, which gave slightly out of tune intervals with all other notes, but the out of tune was barely noticeable, and not as obvious as in the wolf fifth.

So the wolf fifth, like an experienced sea wolf, led the musical ship to very unexpected shores – a uniformly tempered system.

A Brief History of Dissonances

What does a brief history of dissonance teach us? What experience can be drawn from a journey of several centuries?

• First, as it turned out, dissonances in the history of music played no less a role than consonances. Despite the fact that they did not like and fought with them, it was they who often gave impetus to the emergence of new musical directions, served as a catalyst for unexpected discoveries.
• Secondly, an interesting trend can be found. With the development of music, people learn to hear consonance in more and more complex combinations of sounds.

Few people now would consider a small second as such a dissonant interval, especially in a melodic arrangement. But just some two and a half thousand years ago it was so. And the triton entered the musical practice, many musical works, even in popular music, are built with the most serious participation of the tritone.

For example, the composition begins with tritones Jimi Hendrix Purple Haze:

Gradually, more and more dissonances move into the category of “not so dissonances” or “almost consonances”. It’s not that our hearing has deteriorated, and we do not hear that the sound of such intervals and chords is harsh or repulsive. The fact is that our musical experience is growing, and we can already perceive complex multi-step constructions as unusual, extraordinary and interesting in their own way.

There are musicians to whom the wolf fifths or commas presented in this article will not seem terrifying, they will treat them as a kind of complex material that you can work with in creating equally complex and original music.

Author – Roman Oleinikov Audio recordings – Ivan Soshinsky