Movable counterpoint |

Movable counterpoint – a type of complex counterpoint, a polyphonic combination of melodies (different, as well as the same, similar, set out in the form of imitation), suggesting the formation of one or several. derivative compounds as a result of a change in the initial ratio by rearranging (moving, shifting) these unchanging melodies. Depending on the method of rearrangement, according to the teachings of S. I. Taneyev, there are three types of P. to .: vertically movable, based on a change in the original. the ratio of melodies in height, – a derivative connection (see musical examples b, c, d, e) is formed by transferring the melody to one or another interval up or down (i.e. vertically); horizontally movable, based on a change in the moment of entry of one melody, voice relative to another, – a derivative connection (see examples f, g) is formed from the displacement of one of the melody. voices for a certain number of measures (beats of a measure) to the right or left (i.e., horizontally);

S. I. Taneev. From the book “Mobile counterpoint of strict writing”.

doubly mobile, combining the properties of the previous 2, – a derivative compound (see examples h, i, j) is formed as a result of simultaneous. changes in the height ratio and the ratio of the moments of entry of melodic. votes (i.e. vertically and horizontally).

In the aesthetic In relation to polyphony, as a modified reproduction of a combination of unchanging elements, as a unity of renewal and repetition, where renewal does not reach a level of a different quality, and repetition is enriched with structural novelty, it turns out to be one of the manifestations of the specificity of polyphonic. thinking (see Polyphony).

The greatest practical value and distribution is vertical-P. to. So, he is technical. polygonal basis. canons of the 1st category (except for those where the voices enter the same interval and in the same direction).

For example, in a quadruple. fp. In the canon of A. V. Stanchinsky, vertical permutations arise, the system of which can be expressed by the following scheme:

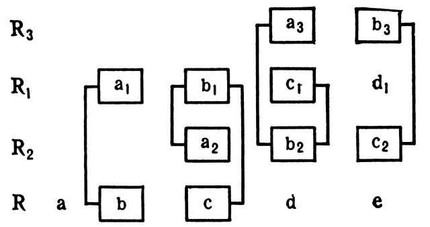
Here Rl in relation to R (see Risposta, Proposta) and R3 in relation to R2 enter the upper octave; R2 enters the lower fifth in relation to R1; 1st initial compound b + a1, its derivatives a2 + b1 and b2 + a3, 2nd initial compound c + b1, its derivatives b2 + c1, ca + b3; a double counterpoint of the duodecym was used (Iv = -11; see below). Permutations in vertical-P. k. – a property of infinite canons (except canons in I will accept) and canonical. sequences of the 1st category. For example, in the jubilant-sounding two-headed. In the endless canon introduced by M. I. Glinka in the climactic conclusion of the coda from the overture to the opera Ruslan and Lyudmila, the voices form the following permutations:

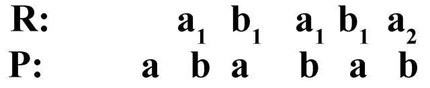
Here: the initial compound b + a1 (bars 28-27, 24-23, 20-19 from the end of the overture), the derivative a + b1 (bars 26-25, 22-21); double octave counterpoint was used (more precisely, fifth decimals, Iv = -14). Examples of vertical-P. because in canon. sequences: two-headed. invention a-moll No. 13 And. C. Bach, bars 3-4 (descending in seconds); the dramatically intense music of the 3rd part of the cantata “John of Damascus” by Taneyev contains rare examples of a sequence in four voices: in number 13 based on the material of the developing part of the theme (a sequence descending in thirds, in fact with doubling of voices), in number 15 based on the initial motive of the theme (complicated by horizontal displacements). Vertical-P. because – an attribute of complex fugues and fugues with a retained opposition. For example, in the double fugue from Kyrie in Requiem V. A. Mozart, two contrasting themes form an initial connection in bars (abbr. – tt.) 1-4; derivative compounds of themes follow almost without interludes in vols. 5-8 (octave permutation), 8-11, 17-20 (in the latter case permutation to duodecime) and so on. Concentration contrapuntal. techniques (vertical permutations of 3 themes) characterizes the reprise of the triple fugue in C from FP. Hindemith’s “Ludus tonalis” cycle, where the initial connection in vols. 35-37 and derivatives in vols. 38-40, 43-45, 46-48. In the Cis-dur fugue from the 1st volume of the Well-Tempered Clavier by I. C. Bach’s theme of the fugue and the retained counterposition form the initial conjunction in tt. 5-7, derivatives in vols. 10-12, 19-21 and beyond. Theme and two retained oppositions in the fugue by D. D. Shostakovich C-dur (No 1) from piano. cycle “24 preludes and fugues” make up the initial connection in vols. 19-26, derived from it in vols. 40-47, 48-55, 58-65, 66-73. Vertical-P. because it is also the most important means of development and shaping in fugues with polyphonically varied interludes. For example, in the c-moll fugue from the 1st volume of Bach’s Well-Tempered Clavier, the 1st interlude (vol. 5-6) – initial, 4th (tt. 17-18) – derivative (Iv = -11, with partial doubling of the lower voice), incl. 19 derivative from the beginning of the 4th interlude (Iv = -14, and from the 1st interlude Iv = -3); 2nd interlude (vols. 9-10) – initial, 5th interlude (tt. 22-23) is a derivative with a permutation in the upper pair of voices. In homophonic and mixed homophonic-polyphonic. vertical-P forms. because can be used in one way or another in any of their sections, eg. when forming the theme in the introduction of the 1st movement of Glazunov’s 5th symphony (8 vols. up to number 2 – initial, 4 t. up to the number 2 – derivative). When exhibiting a side theme in the 1st movement of the 4th symphony by P. AND. Tchaikovsky (the original begins in vol. 122, derivative incl. 128) vertical permutation is a way of melodic. saturation of the lyric. music. Sometimes vertical movements are used in the middle constructions of simple forms (L. Beethoven, fp. sonata op. 2 No 2, Largo appassionato: the original is in the middle of the two-part form, i.e. 9, derivatives – in vols. 10 and 11); in sonata developments, this is one of the most important and widely used means of motivic development (for example, in the 1st movement from the Es-dur quartet by V. A. Mozart, K.-V. 428: original – vols. 85-86, derivatives – vols. 87-88, 89-90, 91-92). Polyphonic is often used. processing of the material with the help of vertical shifts in the reprise sections, where they contribute to the renewal of the sound (for example, in Scriabin’s poem op. 32 No 1 Fis-dur, derivative incl. 25). Often vertical permutations are used in conclusions. sections of the form (for example, in Glinka’s Aragonese Jota code: the original is the number 24, the derivative is 25). Vertical-P. because – one of the most commonly used polyphonic means. variations (for example, in the 3rd movement from Borodin’s D-dur quartet: the initial in the reprise is the number 4, or so on. 111, derivative – number 5 or so on. 133; in No. 14 from Shchedrin’s “Polyphonic Notebook” – a derivative, incl.

The scope of the horizontally movable and doubly movable counterpoints is more limited. T. n. “counterpoint with and without pauses” from P. Mulu’s mass (mentioned by S. I. Taneyev in “Mobile counterpoint” and reproduced in issue 1 of M. V. Ivanov-Boretsky’s Musical-Historical Reader, No 42) remains the only in its own way an example of music. production, entirely based on horizontally-P. k.: polyphonic. the piece can be performed in 2 versions – with pauses (original) and without them (derivative); this rarity serves as a good illustration of the working methods of the masters of the era of austere style. It is more significant that the technique of horizontal and doubly-P. k. underlies some canons of the 2nd category (for example, sounding like the pinnacle of development from the 1st part of the 5th symphony of D. D. Shostakovich, a double canon, where the main and secondary themes are combined, number 32) and canonical . sequences of the 2nd category (for example, in the 2nd part of Myaskovsky’s quartet No. 3, vol. 70 et seq.). Practically most often the specified types of P. to. meet in stretches of fugues with variable distances of introductions. For example, the ricercar-like fugue in C-dur from the 1st volume of Bach’s Well-Tempered Clavier actually consists of progressively more complex strettas; in Credo (No 12) from the Mass in h-moll by J. S. Bach, the original – vols. 4-9, derivatives – vols. 17-21, 34-37. In the fugue from Ravel’s Tomb of Couperin suite, extremely complex movements in strettas create soft dissonant sounds characteristic of this composer: tt. 35-37 – initial (stretta on the topic in direct motion with an entry distance of two eighths); tt. 39-41 – derivative in vertically reversible counterpoint; TT. 44-46 – derivative in incomplete vertically reversible counterpoint; tt. 48-50 – derived from the previous one with a horizontal offset (the entry distance is the eighth); tt. 58-60 – a derivative in the form of a three-goal. stretches in doubly-P. to.

Horizontal movements are sometimes found in fugues with a retained counterposition (e.g., in the gis-moll fugues from vol. 1, As-dur and H-dur from vol. 2 of Bach’s Well-Tempered Clavier; in the final fugue from the concerto for 2 FP Stravinsky).

Exclude. grace distinguishes horizontal movements in the music of W. A. ​​Mozart, for example. in sonata D-dur, K.-V. 576, vols. 28, 63 and 70 (the entry distance is respectively one-eighth, six-eighths and three-eighths with a vertical permutation).

Great art. different-dark horizontal movements are important, for example. in grand fugue Es-dur for organ by J. S. Bach, BWV 552, vol. 90 et seq.; in the 2nd movement of Glazunov’s 7th symphony, 4 measures up to number 16. In the final fugue of the string quintet G-dur op. 14 Taneyev the themes of the double fugue in the derivative connection are carried out with a horizontal displacement (by 2 tons) and a vertical permutation:

On a par with P. to. should be put a kind of complex counterpoint – counterpoint that allows doubling: a derivative compound is formed by doubling one (see examples k, 1) or all (see example m) voices with imperfect consonances (in music of the 20th century – there are any other doublings up to clusters). According to the technique of composing, the counterpoint, which allows doubling, is very close to vertical-P. to., because the doubling voice is essentially the result of a vertical permutation of the doubling interval – a third, a sixth, a decimal. The use of doubling in derivative compounds gives a feeling of compaction, massiveness of sound; e.g. in prelude and fugue for fp. Glazunov, op. 101 No 3 the recapitulation of the themes of the double fugue in m. 71 is the original, in m. 93 is a derivative with an octave vertical permutation and with doubling of voices; in Variation VI from Variations on a Theme of Paganini for two pianos. Lutoslavsky in the original, the upper voice moves with tertian doubling, the lower one with major triads, in the inexact derivative (v. 6) the upper voice moves with parallel minor triads, the lower one with thirds.

P. to. and counterpoint, which allows doubling, can be combined with reversible counterpoint (for example, in the development of the finale of the symphony C-dur “Jupiter” by W. A. ​​Mozart, the canonical imitation in direct movement in bars 173-175 is the initial, in bars 187-189 – a derivative with inversion and vertical permutation of voices, in bars 192-194 – a derivative with vertical permutation and with only one voice inverted), sometimes in combination with such forms of melodic. transformations, such as increase, decrease, forming very complex constructions. So, the variation of polyphonic. combinations in means. measure determines the appearance of music FP. quintet g-moll (op. 30) Taneyev: see, for example, the numbers 72 (original) and 78 (derivative with increase and horizontal movement), 100 (derivative in doubly P. k.), 220 – in the finale ( combination of the main theme with its quadruple increase).

The theory of counterpoint and counterpoint, which allows doubling, was exhaustively developed by S. I. Taneev in his fundamental work “Mobile counterpoint of strict writing”. The researcher establishes a notation that allows mathematical. by accurately characterizing the movement of voices and determining the conditions for writing P. to. Some of these designations and concepts: I – upper voice, II – lower voice in two- and middle in three-voices, III – lower voice in three-voices (these designations are preserved in derivatives); 0 – prima, 1 – second, 2 – third, 3 – quart, etc. (such digitization of intervals is necessary for their addition and subtraction); h (short for lat. horisontalis) – horizontal movement of the voice; Ih (short for lat. index horisontalis) – an indicator of horizontal movement, determined in cycles or beats (see examples f, g, h, i, j); v (short for lat. verticalis) – vertical movement of the voice. The movement of the upper voice up and down is measured by the corresponding interval with a positive value, the movement of the upper voice down and lower up by the interval with a minus sign (for example, IIV=2 – movement of the upper voice up by a third, IIV=-7 – movement of the lower voice up by octave). In vertical-P. j. a permutation, with which the upper voice of the original connection (the formula of the original in two-voice I + II) retains the position of the upper one in the derivative, is called direct (see examples b, c; a figure denoting a direct permutation in two-voice:

). A permutation, in which the upper voice of the original occupies the position of the lower one in the derivative, is called the opposite (see examples d, e; its image:

).

Two-headed polyphonic a compound that allows vertical permutations (not only opposite, but also – in contrast to the common inaccurate definition – and direct), called. double counterpoint (German doppelter Kontrapunkt); e.g., in a double Inventions E-dur No 6 J. S. Bach original – in vols. 1-4, derivative – in vols. 5-8, IV=-14 + II V=-7

). Three-headed. a connection that allows 6 combinations of voices (any of the original voices can be upper, middle or lower in the derivative connection) is called triple counterpoint (German dreifacher Kontrapunkt, Tripelkontrapunkt). Figures denoting permutations in triphony:

For example, in a three-goal Inventions f-moll No 9 J.S. Bach: the original – in vols. 3-4, derivatives – in vols. 7-8

in No. 19 from Shchedrin’s “Polyphonic Notebook” – a derivative in v. 9. The same principle underlies the little-used. quadruple counterpoint (German vierfacher Kontrapunkt, Quadrupelkontrapunkt), allowing 24 voice positions (see, for example, numbers 5, 6, 7 in the 1st part of the cantata “John of Damascus”; numbers 1, 2, 3, 4 in the conclusion. in the double choir No. 9 of the cantata “After the Reading of the Psalm” by Taneyev, and in the fugue in e-moll from the cycle “24 Preludes and Fugues” for pianoforte Shostakovich – vols. 15-18 and 36-39). A rare example of five counterpoint — the code of the finale of the symphony C-dur (“Jupiter”) by W. A. ​​Mozart: the original in vols. 384-387, derivatives in vols. 387-391, 392-395, 396-399, 399-402; permutation scheme:

Algebraic. the sum of the intervals of movement of both voices (in two-voice; in three- and polyphony – for each pair of voices) is called the indicator of vertical movement and is denoted by Iv (short for Latin index verticalis; see examples b, c, d, e). Iv is the most important definition in the teachings of S.I. Taneev, because he characterizes the norms for the use of intervals formed between polyphonic voices. tissues, and features of voice leading. For example, when writing the initial compound in double counterpoint of the decimal (i.e. Iv = -9), only the opposite and indirect movement of voices is assumed within the framework of strict writing, and the retention of a quart by the upper voice and none by the lower voice is not allowed in order to avoid sounds in the derivative compound prohibited by the rules of this style. The permutation can be carried out at any interval and, therefore, Iv can have any value, however, in practice, three types of permutations are most common: double counterpoint decimals (Iv = -9 or -16), duodecimes (Iv = -11 or -18) and especially double octave counterpoint (Iv = -7 or -14). This is explained by the fact that when permuting the double counterpoint of the octave, decima and duodecima, the harmonic changes little in the derivatives. the essence of the original connection (consonant intervals of the original mostly correspond to consonant intervals in the derivative; the same dependence exists between dissonances). The ability to make vertical permutations on decomp. intervals (i.e. use different values ​​of Iv) constitutes specifically contrapuntal art. a means that allows the composer to subtly diversify the sonority. One of the outstanding examples is the g-moll fugue from the 2nd volume of Bach’s Well-Tempered Clavier: the theme and the withheld opposition form the initial conjunction in bars. 5-9; derivative in tt. 13-17 (Iv=-14), 28-32 (Iv=-11), 32-36 (Iv=-2) and 36-40 (Iv=-16); in addition, in tt. 51-55 in the derivative the theme is doubled by the sixth from above (Iv = +5), in tt. 59-63 permutation at Iv=-14 with doubling the theme by a third from below, and counteraddition by a third from above (Iv = -2). In music after Bach and up to the 20th century. more often a relatively simple octave permutation is used; however, composers, as the harmonica grows. freedoms use relatively little-used indicators in the past. In particular, they are found in the canon. sequences where a derivative compound is formed between the risposta and the re-entry of the proposta: for example, in the 2nd movement of Mozart’s D-dur quartet, K.-V. 499, vols. 9-12 (Iv = -13); in the 1st movement of Glazunov’s Symphony No. 8, number 26, vols. 5-8 (Iv = -15); in the overture to the opera “Meistersingers of Nuremberg”, vol. 7 (Iv = -15) and vol. 15 (Iv = -13); in the 1st picture of the 3rd d. “Tales of the invisible city of Kitezh”, number 156, vols. 5-8 (Iv=-10); in the 1st movement of Myaskovsky’s Quartet No. 12, vols. 6-11, 17-21 (Iv = -17).

H. A. Rimsky-Korsakov. “The Tale of the Invisible City of Kitezh and the Maiden Fevronia”, act III, 1st scene.

The connection established by S. I. Taneyev with the canon (in the book “The Doctrine of the Canon”) made it possible to accurately classify and scientifically determine the principles of decomp. canon forms. P.’s theory to. served as the basis for the further development of the teachings of Taneyev in owls. musicology (S. S. Bogatyrev, “Double Canon” and “Reversible Counterpoint”).

References: Taneev S. I., Movable counterpoint of strict writing, Leipzig, 1909, M., 1959; his own, Doctrine of the Canon, M., 1929; Ivanov-Boretsky M.V., Musical and historical reader, vol. 1, M., 1929; Bogatyrev S. S., Double canon, M.-L., 1947; his, Reversible counterpoint, M., 1960; Dmitriev A. N., Polyphony as a factor of shaping, L., 1962; Pustylnik I. Ya., Movable counterpoint and free writing, L., 1967; Jadassohn S., Lehrbuch des einfachen, doppelten, drei- und vierfachen Contrapunkts, Lpz., 1884, id., in his Musikalische Kompositionslehre, Tl. 1, Bd 2, Lpz., 1926; Riemann H., Lehrbuch des einfachen, doppelten und imitierenden Kontrapunkts, Lpz., 1888. 1921; Prout, E., Double counterpoint and canon, L., 1891, 1893.

V. P. Frayonov